2024. 1. 21. 15:00ㆍAlgorithm/with Java
0. 문제
SW Expert Academy
SW 프로그래밍 역량 강화에 도움이 되는 다양한 학습 컨텐츠를 확인하세요!
swexpertacademy.com
1. 문제 이해
최장 증가 부분 수열에 관한 문제이다.
별다른 접근 방법이 생각나지 않기 때문에 모든 경우의 수를 실행하고 그 결괏값을 비교하기로 했다.
a1, a2, a3, a4, a5, …, an 수열이 주어진다면 수열의 크기는 n이다.
수열에서 파생될 수 있는 순서가 바뀌지 않는 모든 부분 순열은 수는 2^n이다.
2. 시간 초과
import java.io.*;
import java.util.StringTokenizer;
class Solution {
static int n;
static int ret;
public static void solve(int[] arr, int depth, int big, int cnt) {
if(depth == n){
ret = Math.max(ret, cnt);
//System.out.println("cnt : " + cnt + " " + "ret : " + ret);
return;
}
if(big < arr[depth]){
//System.out.print(arr[depth] + " ");
solve(arr, depth + 1, arr[depth], cnt + 1);
}
solve(arr, depth + 1, big, cnt);
}
public static void main(String args[]) throws Exception {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st = new StringTokenizer(br.readLine());
int T = Integer.parseInt(st.nextToken());
for(int tc=1; tc<=T; tc++) {
ret = 0;
st = new StringTokenizer(br.readLine());
n = Integer.parseInt(st.nextToken());
int[] arr = new int[n];
st = new StringTokenizer(br.readLine());
for(int i=0; i<n; i++){
arr[i] = Integer.parseInt(st.nextToken());
}
solve(arr, 0, 0, 0);
System.out.println("#" + tc + " " + ret);
}
br.close();
}
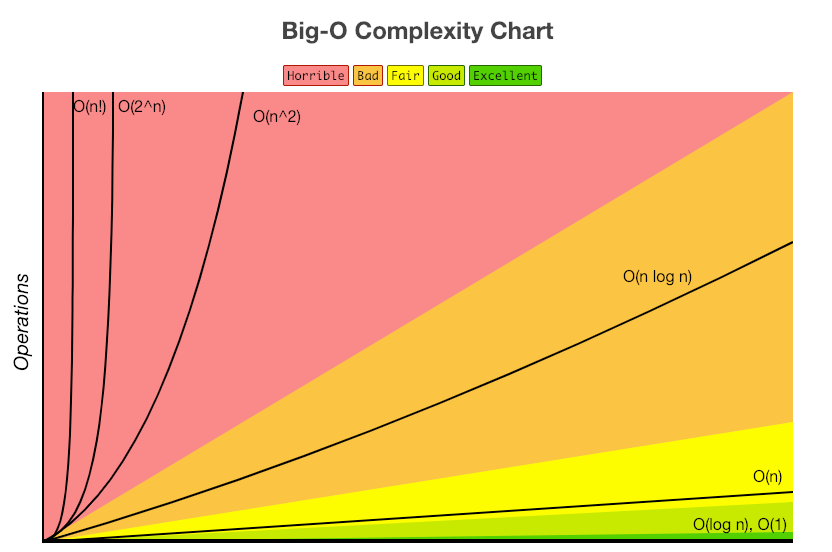
}O(2^n)의 시간복잡도로는 통과할 수 없다.
N = 1000일 때 10개의 테스트케이스를 2초 안에 통과하기 위해서는 하나의 테스트케이스를 0.2초 안에 통과해야 한다.
1억을 1초로 계산할 경우 O(2^n)은 2^1000이다. 어림도 없다.
반면 O(n^2)만 해도 1,000,000으로 대략 0.01초이다.
대략적으로 계산했을 때 O(2^n)보다는 O(n^2)으로 풀어야 한다.
3. 개선
가. O(n^2)
시간을 줄이기 위해서 동적 프로그래밍을 사용하여 최장 증가 부분 수열의 길이를 계산해야 한다.
문제를 작게 나누어 해결하고, 그 결괏값을 저장해 중복 계산을 피한다.
i번째까지의 최장 부분 증가수열의 크기는 다음과 같은 과정을 통해서 구할 수 있다.
- 0에서
i-1까지의 위치한 숫자들 가운데i번째 숫자보다 작은 숫자를 찾는다. - 해당 숫자들 가운데서 최장 부분 증가수열의 크기가 가장 큰 숫자를 찾는다.
- 해당 숫자의 최장 부분 증가 서열의 크기에
1을 더한 값이i번째까지의 최장 부분 증가 수열이 된다.
import java.io.*;
import java.util.StringTokenizer;
public class Solution {
public static int solve(int n, int[] arr){
int[] lis = new int[n];
for(int i=0; i<n; i++){
lis[i] = 1;
for(int j=0; j<i; j++){
if(arr[j] < arr[i] && lis[j] >= lis[i]){
lis[i] = lis[j] + 1;
}
}
}
int max = 0;
for(int num : lis){
max = Math.max(max, num);
}
return max;
}
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader((new InputStreamReader(System.in)));
StringTokenizer st = new StringTokenizer(br.readLine());
int T = Integer.parseInt(st.nextToken());
for(int tc=1; tc<=T; tc++){
st = new StringTokenizer(br.readLine());
int n = Integer.parseInt(st.nextToken());
int[] arr = new int[n];
st = new StringTokenizer(br.readLine());
for(int i=0; i<n; i++){
arr[i] = Integer.parseInt(st.nextToken());
}
int ret = solve(n, arr);
System.out.println("#" + tc + " " + ret);
}
br.close();
}
}lis[i]은0에서부터i까지 요소를 사용해서 만들 수 있는 최장 증가 부분 수열의 길이를 저장한다.if(arr[j] < arr[i] && lis[j] >= lis[i]){
:i보다 앞에 위치한 숫자들 가운데 자신보다 작은 수를 찾는다.
: 찾은 수들 가운데서 최장 증가 부분 수열의 크기가 가장 큰 값을 활용한다.lis[i] = lis[j] + 1;
: 1을 더한 값을 저장한다.
: 다음 숫자의 최장 부분 증가수열을 구하는 데 사용된다.
결괏값을 저장하고 재활용하기 때문에 시간 복잡도는 O(n^2)으로 줄어든다.
나. O(NlogN)
O(NlogN)의 시간 복잡도로 푸는 방법을 추가한다.
import java.io.BufferedReader;
import java.io.InputStreamReader;
import java.util.Arrays;
import java.util.StringTokenizer;
// 최장 증가 부분 수열
public class SWEA3307_2 { //122ms
static int N, ret;
static int[] arr, lis;
public static void main(String[] args) throws Exception {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st = new StringTokenizer(br.readLine());
StringBuffer sb = new StringBuffer();
int T = Integer.parseInt(st.nextToken());
for(int tc=1; tc<=T; tc++){
init(br, st);
solve();
sb.append("#").append(tc).append(" ").append(ret).append("\\n");
}
System.out.println(sb);
br.close();
}
private static void init(BufferedReader br, StringTokenizer st) throws Exception {
st = new StringTokenizer(br.readLine());
N = Integer.parseInt(st.nextToken());
arr = new int[N];
lis = new int[N];
st = new StringTokenizer(br.readLine());
for(int i=0; i<N; i++){
arr[i] = Integer.parseInt(st.nextToken());
}
//debug
//System.out.println(Arrays.toString(arr));
}
private static void solve() {
int idx = 0, point;
for(int i : arr){
point = Arrays.binarySearch(lis, 0, idx, i);
if(point < 0) point = -(point + 1); // 기존에 없는 경우
lis[point] = i;
if(point==idx)++idx;
// debug
//System.out.println(Arrays.toString(lis));
}
ret = idx;
}
}
[Java] LIS, LCS
1. LIS란? Longest Increasing Subsequence최장 증가 부분 수열어떤 임의의 수열이 주어질 때, 이 수열에서 몇 개의 수를 제거하여 부분 수열을 만든다. 이때 만들어진 부분수열 중 오름차순으로 정렬된 가
ramen4598.tistory.com
문제를 풀기 이전에 우선 테스트케이스의 수, N의 크기, 주어진 시간을 확인하자.
이를 활용해서 시간 복잡도의 커트라인을 파악하자.
'Algorithm > with Java' 카테고리의 다른 글
| [Java] 순열과 조합 (1) | 2024.01.31 |
|---|---|
| [알고리즘] 풀었던 문제 (241031) (0) | 2024.01.31 |
| [알고리즘] 풀었던 문제 (240131) (0) | 2024.01.31 |
| [알고리즘] 9658. 돌 게임 4 (0) | 2024.01.23 |
| [Java] 입출력 (0) | 2024.01.21 |