[Java] 서로소 집합
2024. 2. 25. 22:58ㆍAlgorithm/with Java
1. 서로소 집합
- Disjoint-set
- 상호 배타 집합
- 서로 중복되는 원소가 없는 집합들.
- 표현
- 연결 리스트
- 트리
- 연산
- 집합들을 식별하기 위해서 특정 멤버를 대표자로 사용한다.
make-set(x): 집합을 생성한다. 전처리 과정에서 단 한번 실행된다.find-set(x):x가 속한 집합을 찾아서 대표자를 반환한다.Union(x, y):x가 속한 집합과y가 속한 집합을 합친다.
Union-Find 연산이 핵심이다.
가. 연결 리스트로 구현
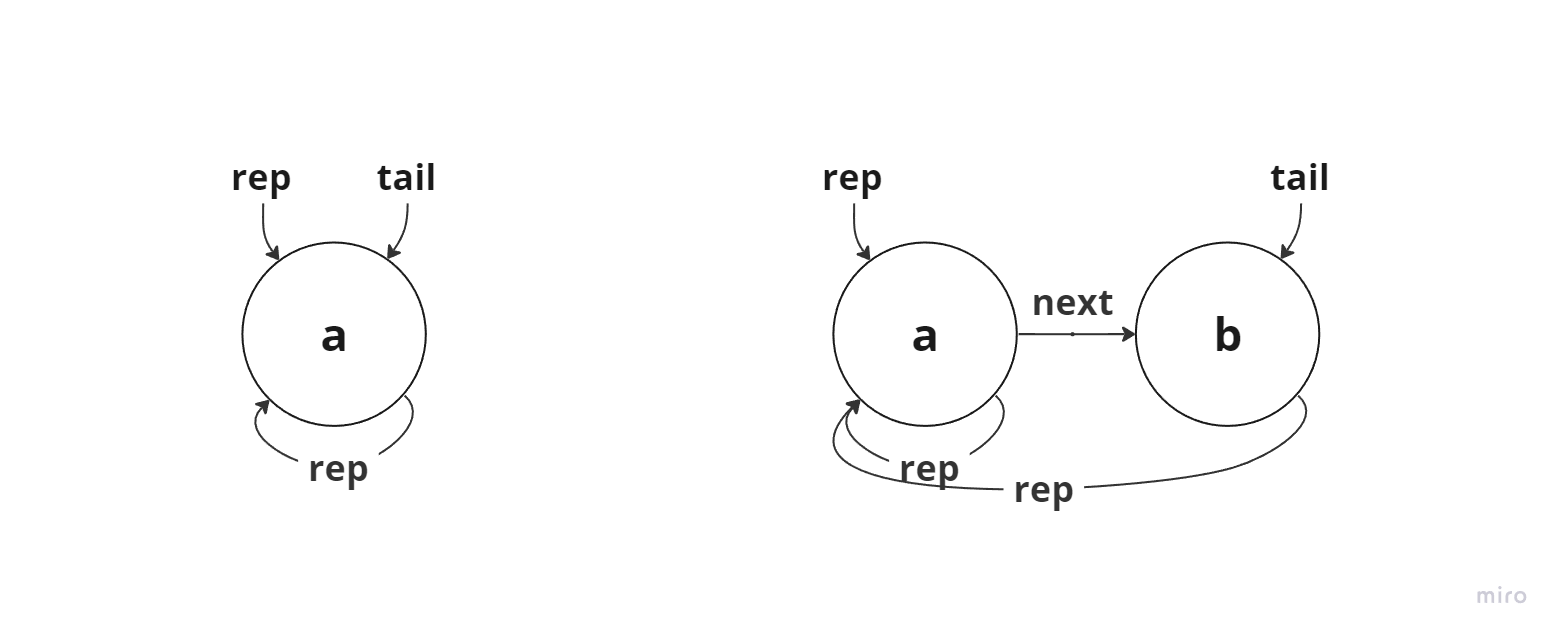
- 같은 집합의 원소들은 하나의 연결리스트로 관리
- 가장 앞의 원소를 대표자로 사용
- 각각의 원소는 자신의 대표자와 다음 원소를 가리키는 2개의 링크를 가진다.
- 연산의 편의성을 위해서
tail을 사용한다.
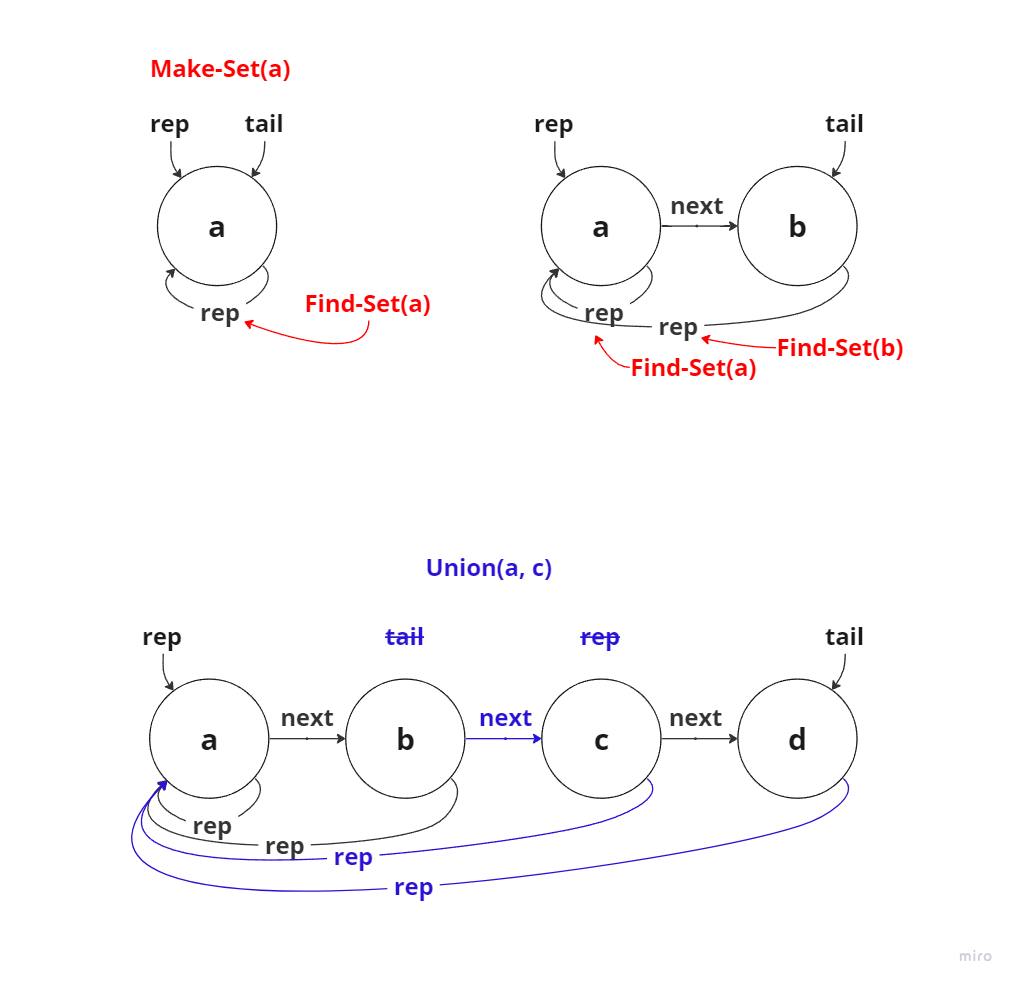
Make-Set(a):a를 대표자(rep)이자tail로 설정하는a만 원소로 가진 연결 리스트 생성.Find-Set(e):e의rep를 반환한다.Union(a, b):a집합의tail뒤로b를 연결한다.rep는a로tail은b의tail로 설정한다.
나. 트리로 구현
연결리스트보다는 트리로 많이 구현한다. (시간 복잡도에서 유리함.)
- 같은 원소는 하나의 트리에 저장한다.
- 루트 노드가 대표자가 된다.
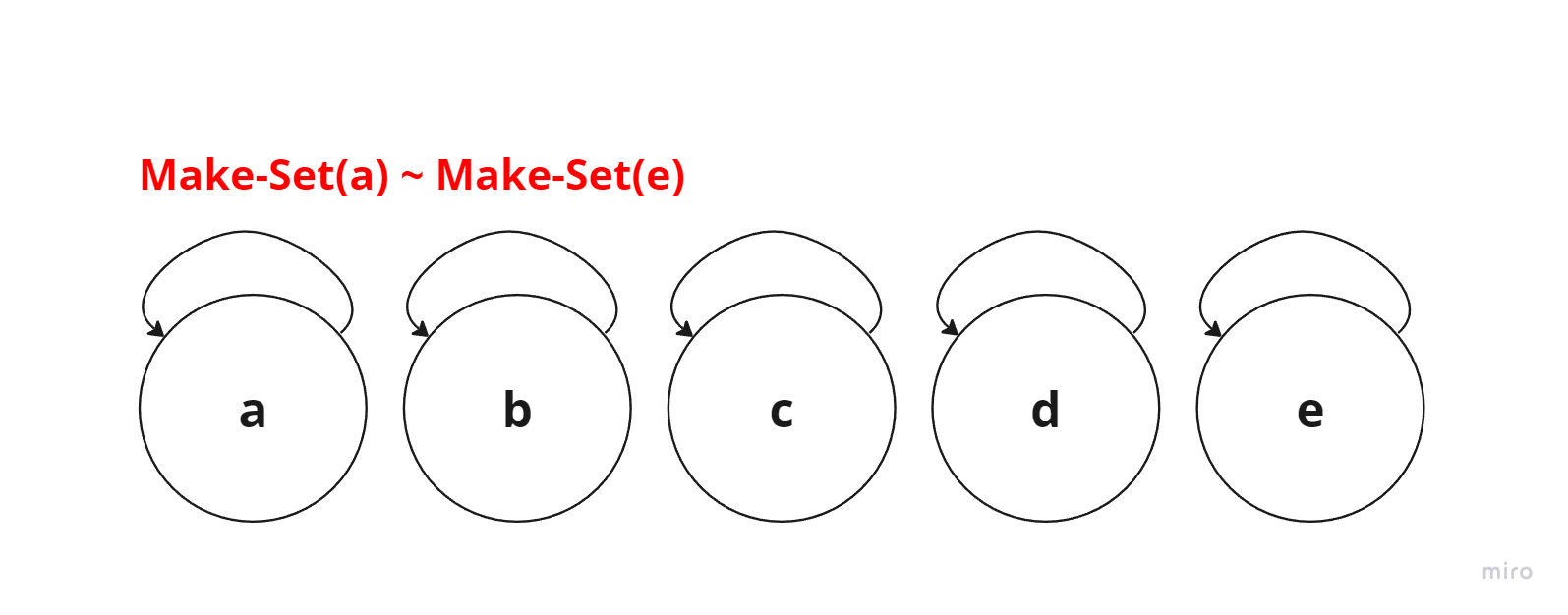
Make-Set(a):a만 노드로 가진 트리 생성. 루트 노드는 자기 자신.
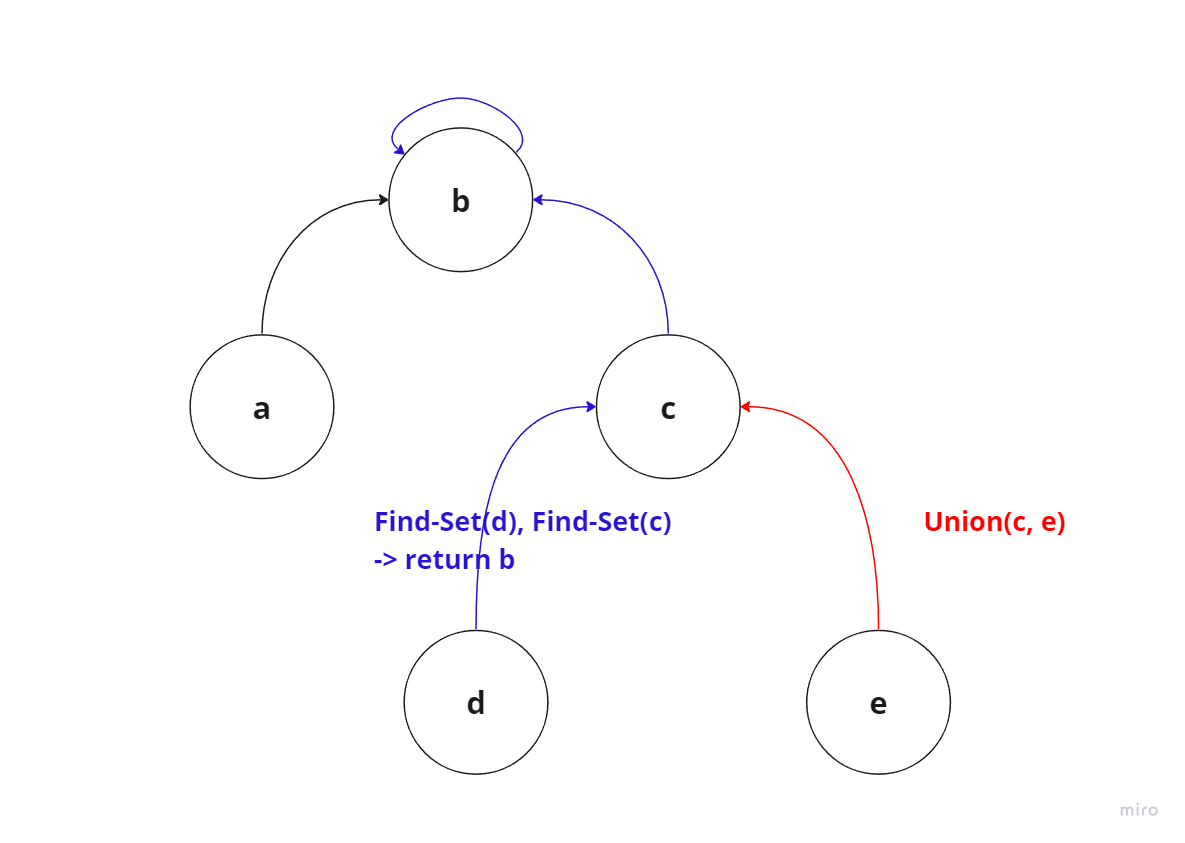
Union(c, e)
:c가 속한 트리의 루트 노드를e가 속한 트리의 루트노드의 부모 노드로 설정.
: 루트노드의 부모 노드만 수정하면 되기 때문에 연결리스트에 비해서 Union 연산이 단순하다.Find-Set(d):d가 속한 트리의 루트 노드b반환.
다. 연산 구현
p[x]:x의 부모 노드의 인덱스를 저장하고 있는 배열
1) Make-Set(x)
유일한 멤버 x를 포함하는 새로운 집합을 생성하는 연산.
Make-Set(x)
p[x] == <- x
2) Find_Set(x)
x를 포함하는 집합을 찾는 연산.
Find-Set(x)
IF x == p[x] : RETURN x // 루트 노드
ELSE : RETURN Find-Set(p[x]) /// 재귀 함수
3) Union(x, y)
x와 y를 포함하는 두 집합을 통합하는 연산.
Union(x, y)
IF Find-Set(y) == Find-Set(x) RETURN
p[Find-Set(y)] <- Find-Set(x)
2. 서로소 집합 - 최적화

최악의 경우 루트 노드를 찾기 위해서 시간 복잡도 O(N) 소요.
두 가지 방법으로 시간 복잡도를 관리할 수 있다.
- 최적화 방법
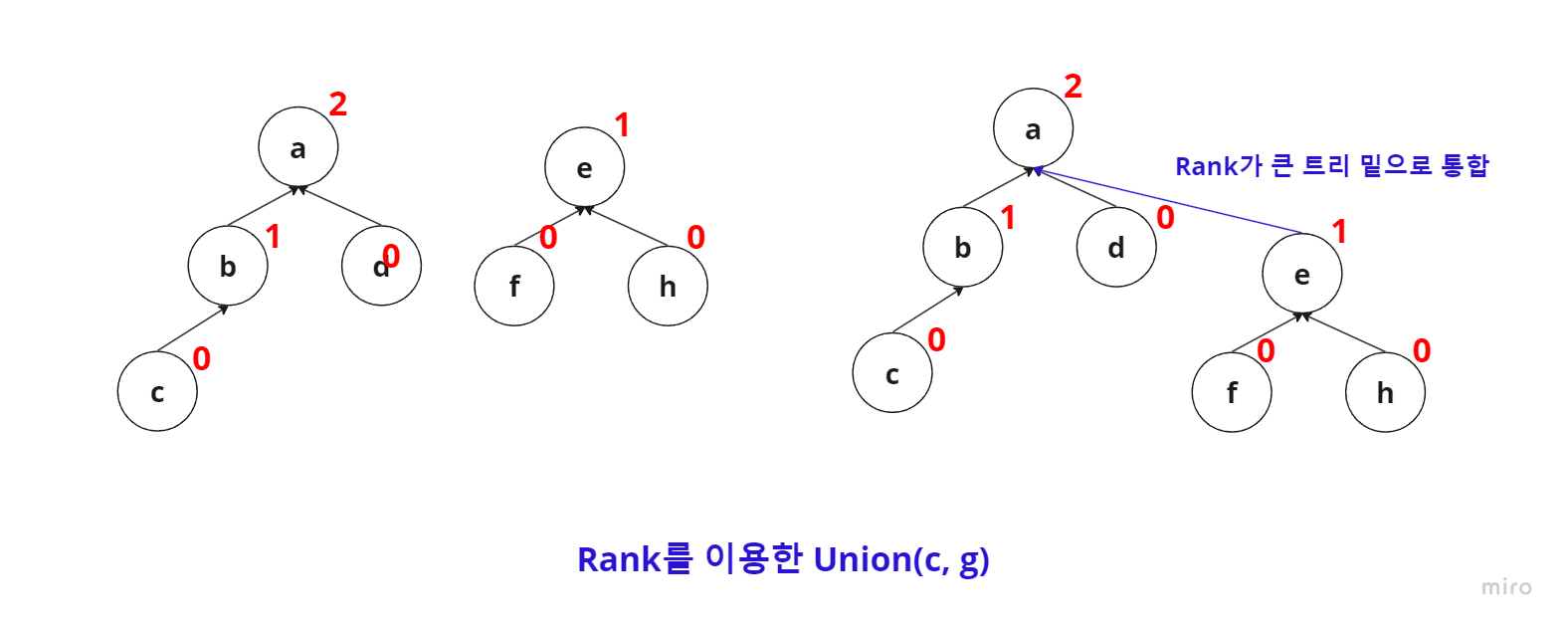
- Rank를 이용한 Union (rank 관리)
: 두 집합이 합칠 때 높이(rank)가 낮은 집합을 높이(rank)가 높은 집합에 붙인다.
: 완벽한 rank 관리가 가능함. - Path compression (경로 압축)
: Find-Set을 행하는 과정에서 만나는 모든 노들들이 직접 root를 가리키도록 포인터를 변경.
: rank 변화의 가능성은 존재하지만 완벽하게 rank가 관리되진 않는다.
- Rank를 이용한 Union (rank 관리)

Find-Set(x)
IF x == p[x] : RETURN x // 루트 노드
~~ELSE : RETURN Find-Set(p[x]) /// Before~~
ELSE : RETURN p[x] = Find-Set(p[x]) // After
Path compression을 수행하는 Find_Set(x)이다.
비교적 구현의 난이도가 낮다.
일반적으로 코딩 테스트에서 rank 관리까진 필요하진 않다.
3. Java 코드
import java.util.Arrays;
public class DisJointSet {
static int N;
static int[] p; // 부모 노드를 저장하는 배열
public static void main(String[] args) {
N = 5;
p = new int[N];
make();
boolean flag = union(2, 3);
System.out.println(flag); // true;
System.out.println(find(3)); // 2
System.out.println(Arrays.toString(p)); // [0, 1, 2, 2, 4]
}
static void make() {
// p배열에 자신의 index 첨자를 값으로 설정
for(int i=0; i<N; i++) {
p[i] = i;
}
}
static int find(int x) {
if(x == p[x]) {
return p[x]; // x;
}
p[x] = find(p[x]); // 경로 압축
return p[x];
// 삼항 연산자
// return (x == p[x]) ? x : (p[x] = find(p[x]));
}
static boolean union(int x, int y) {
int xRoot = find(x);
int yRoot = find(y);
if(xRoot == yRoot) { // 결합 불가
return false;
}
p[yRoot] = xRoot; // 결합
return true;
}
}
'Algorithm > with Java' 카테고리의 다른 글
| [알고리즘] 3289. 서로소 집합 (0) | 2024.02.25 |
|---|---|
| [Java] 최소 신장 트리 (0) | 2024.02.25 |
| [알고리즘] 풀었던 문제 (240220 ~ 22) (0) | 2024.02.25 |
| [알고리즘] 1260. DFS와 BFS (0) | 2024.02.25 |
| [알고리즘] 2252. 줄 세우기 (0) | 2024.02.25 |