[Java] Knapsack
2024. 6. 12. 21:29ㆍAlgorithm/with Java
1. Knapsack
Knapsack 문제는 조합 최적화 문제의 일종으로 주어진 물건들의 가치와 무게, 그리고 배낭의 총용량이 주어졌을 때, 배낭에 넣은 물건들의 가치의 합이 최대가 되도록 하는 물건들의 부분집합을 찾는 문제이다.
동적 계획법(Dynamic Programming)으로 풀 수 있다.
- 0-1 Knapsack
: 각 물건을 배낭에 넣거나 넣지 않거나 두 가지 경우만 고려하는 문제. - 0-N Knapsack
: 각 물건을 배낭에 여러 개 넣을 수 있는 문제입니다. - Fractional Knapsack
: 각 물건을 배낭에 일부분만 넣을 수 있는 문제입니다.
: 무게 대비 가치가 높은 물건부터 배낭에 담는 탐욕 알고리즘(Greedy Algorithm)을 이용하여 풀 수 있다.

import java.io.BufferedReader;
import java.io.InputStreamReader;
import java.util.StringTokenizer;
// 평범한 배낭
public class Main {
static int N, K, ret; // 개수, 최대 무게, 출력값
static int[] W, V; // 물건의 무게, 가치
static int[][] dp;
public static void main(String[] args) throws Exception {
init();
solve();
System.out.println(ret);
}
static void init() throws Exception {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st = new StringTokenizer(br.readLine());
N = Integer.parseInt(st.nextToken());
K = Integer.parseInt(st.nextToken());
W = new int[N+1];
V = new int[N+1];
for(int i=1; i<=N; i++) {
st = new StringTokenizer(br.readLine());
W[i] = Integer.parseInt(st.nextToken());
V[i] = Integer.parseInt(st.nextToken());
}
ret = 0;
// dp 초기화
dp = new int[N+1][K+1];
}
static void solve() {
// 상향식 dp
for(int y=1; y<=N; y++) {
for(int x=1; x<=K; x++) {
if(x >= W[y]) { // y번 물건을 추가할 수 있다면
dp[y][x] = Math.max(dp[y-1][x], dp[y-1][x-W[y]] + V[y]);
}else { // 추가할 수 없다면
dp[y][x] = dp[y-1][x];
}
}
}
ret = dp[N][K];
}
}
2. 공간 복잡도 개선
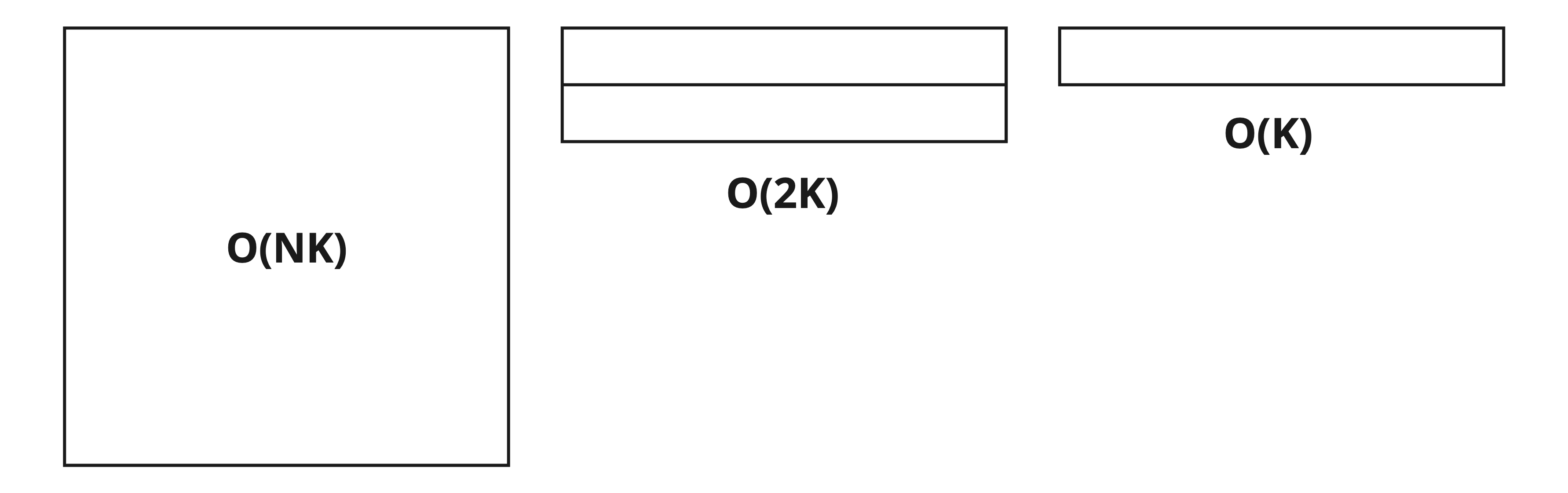
기존의 동적 계획법(DP)은 O(NK)의 공간 복잡도를 가지고 있다.
(여기서 N은 물건의 개수, K는 배낭의 최대 무게를 나타냅니다.)
기존의 DP table보다 작은 공간복잡도를 가지도록 개선할 수 있다.
가. 2차원 배열
현재 최적해를 구하기 위해서 필요한 것은 직전 최적해 뿐이다.

현재 최적해와 직전 최적해를 저장할 2개의 배열만 있으면 충분하다.
int[][] dp = new int[2][K+1]; // 2행을 가진 2차원 DP 테이블 초기화
for (int y = 1; y <= N; y++) {
for (int x = 1; x <= K; x++) {
if (x >= W[y]) { // y번째 물건을 추가할 수 있다면
dp[y % 2][x] = Math.max(dp[(y - 1) % 2][x], dp[(y - 1) % 2][x - W[y]] + V[y]);
} else { // 추가할 수 없다면
dp[y % 2][x] = dp[(y - 1) % 2][x];
}
}
}
ret = dp[N % 2][K]; // 최종 최적해공간 복잡도를 O(NK)에서 O(2K) = O(K)로 줄일 수 있다.
(여기서 N은 물건의 개수, K는 배낭의 총용량을 나타냅니다.)
나. 1차원 배열
동적 프로그래밍(DP) 테이블의 공간 복잡도를 극한으로 줄여서 1차원 배열만 사용해서 문제를 풀 수 도 있다.

- 0-N Knapsack
: DP 테이블을 앞에서부터 채워야 합니다.
: 뒤에 것은 앞의 것의 영향을 받기 때문에 같은 물건을 여러 번 담는 것과 같은 효과를 가진다. - 0-1 Knapsack
: DP 테이블을 뒤에서부터 채웁니다.
: 뒤에서부터 채우면 뒤에 것이 앞의 것의 영향을 받지 않기 때문에 물건을 한 번만 담는 것과 같은 효과를 가진다.
다음은 예시 코드입니다:
int[] dp = new int[K+1]; // 1차원 DP 테이블 초기화
for (int y = 1; y <= N; y++) {
for (int x = K; x >= W[y]; x--) { // 끝에서부터 시작
dp[x] = Math.max(dp[x], dp[x - W[y]] + V[y]);
}
}
ret = dp[K]; // 최종 최적해공간 복잡도는 O(K)입니다.
'Algorithm > with Java' 카테고리의 다른 글
| [Java] 플로이드 워샬 (0) | 2024.06.13 |
|---|---|
| [Java] LIS, LCS (0) | 2024.06.13 |
| [알고리즘] 2457. 공주님의 정원 (1) | 2024.03.05 |
| [알고리즘] 풀었던 문제 (240227 ~ 29) (0) | 2024.03.05 |
| [알고리즘] 2383. 점심식사시간 (0) | 2024.03.02 |