[Java] 최단 경로
2024. 2. 27. 00:43ㆍAlgorithm/with Java
1. 최단 경로 알고리즘
간선의 가중치가 있는 그래프에서 두 정점 사이의 경로들 중에 간선의 가중치의 합이 최소인 경로.
2. Dijkstra 알고리즘
- 음의 가중치가 없는 그래프의 한 정점에서 다른 정점들까지의 최단 거리 비용을 구하는 알고리즘.
- 시간 복잡도
: 반복문으로 구현 시O(V^2)
: PQ로 구현 시O(ElogE)

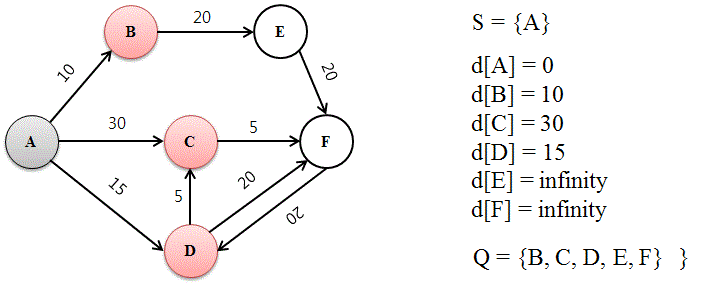
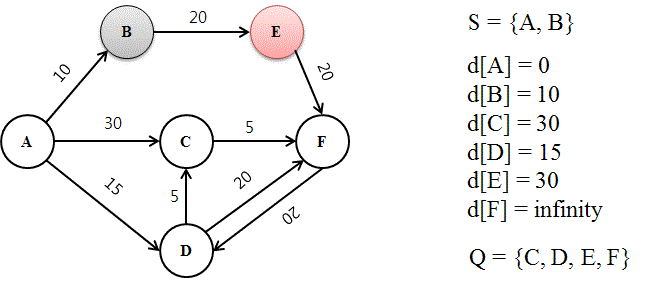
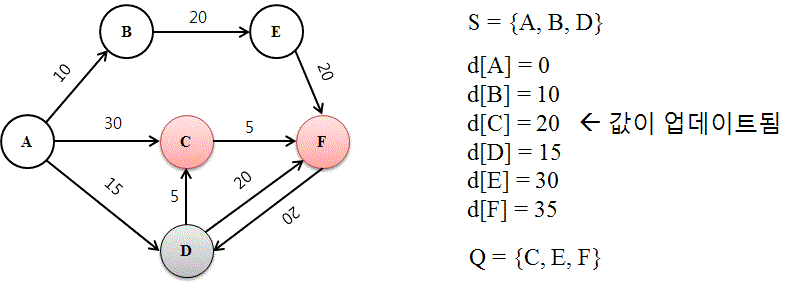
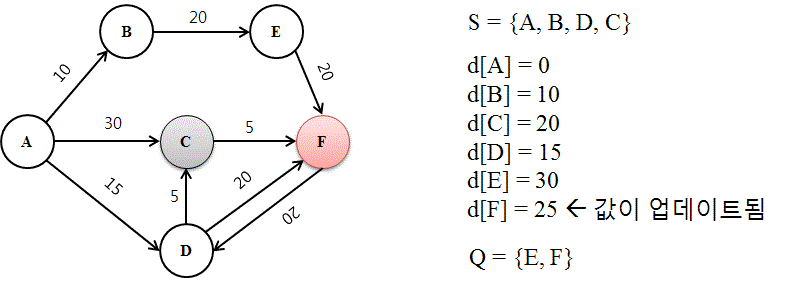
가. 반복문으로 구현
- 시간 복잡도 : 반복문으로 구현 시
O(V^2)
import java.io.BufferedReader;
import java.io.InputStreamReader;
import java.util.Arrays;
import java.util.StringTokenizer;
public class dijkstraTest {
static class Node {
int vertex, weight;
Node next;
public Node(int vertex, int weight, Node next) {
super();
this.vertex = vertex;
this.weight = weight;
this.next = next;
}
@Override
public String toString() {
return "Node [vertex=" + vertex + ", weight=" + weight + ", next=" + next + "]";
}
}
public static void main(String[] args) throws Exception {
BufferedReader in = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st = new StringTokenizer(in.readLine().trim());
int V = Integer.parseInt(st.nextToken()); //정점 갯수
int E = Integer.parseInt(st.nextToken()); //정점 갯수
st = new StringTokenizer(in.readLine().trim());
int start = Integer.parseInt(st.nextToken());;
int end = Integer.parseInt(st.nextToken());; //도착점 인덱스
final int INF = Integer.MAX_VALUE;
Node[] adjList = new Node[V];
int[] minDistance = new int[V];
boolean[] vis = new boolean[V];
int from, to, weight;
for(int i=0; i<E; i++) {
st = new StringTokenizer(in.readLine());
from = Integer.parseInt(st.nextToken());
to = Integer.parseInt(st.nextToken());
weight = Integer.parseInt(st.nextToken());
adjList[from] = new Node(to, weight, adjList[from]);
}
Arrays.fill(minDistance, INF);
minDistance[start] = 0;
int min = 0, stopOver = 0;
for(int i=0; i<V; i++) {
// step1. 미방문 정점 중 출발지에서 가장 가까운 정점 선택
min = INF;
stopOver = -1;
for(int j=0; j<V; j++) {
if(!vis[j] && min > minDistance[j]) {
min = minDistance[j];
stopOver = j;
}
}
if(stopOver == -1) break;
vis[stopOver] = true;
if(stopOver == end) break;
// step2. 미방문 정점들에 대하여 선택된 경유지를 거쳐서 가는 비용과 기존 최소 비용을 비교하여 업데이트
for(Node tmp = adjList[stopOver]; tmp != null; tmp = tmp.next) {
if(!vis[tmp.vertex] && minDistance[tmp.vertex] > min + tmp.weight) {
minDistance[tmp.vertex] = min + tmp.weight;
}
}
}
//System.out.println(Arrays.toString(minDistance));
System.out.println(minDistance[end] != INF ? minDistance[end] : -1);
}
}min = INF;: 인접하지 않다면 가중치로 엄청 큰 값을 넣는다.
다익스트라 알고리즘은 음의 가중치가 없는 그래프를 전제조건으로 가진다.
음의 가중치가 없기 때문에 매 순간 시작점에서 가장 가까운 정점의 비용은 더 이상 감소하지 않는다.
// step2. 미방문 정점들에 대하여 선택된 경유지를 거쳐서 가는 비용과 기존 최소 비용을 비교하여 업데이트
for(Node tmp = adjList[stopOver]; tmp != null; tmp = tmp.next) {
if(!vis[tmp.vertex] && minDistance[tmp.vertex] > min + tmp.weight) {
minDistance[tmp.vertex] = min + tmp.weight;
}
}Prim과 굉장히 비슷하다.
Prim과의 차이점은 최소 비용을 계산하는 기준점에 있다.
Prim은 트리에 포함된 모든 정점과 트리에 포함되지 않은 정점 간에 최소 비용을 계산한다.
하지만 Dijkstra는 오로지 시작점과 방문하지 않은 정점 간에 최소 비용을 계산한다.
나. PQ로 구현하기
- 시간 복잡도 : PQ로 구현 시
O(ElogE)
import java.io.BufferedReader;
import java.io.InputStreamReader;
import java.util.Arrays;
import java.util.StringTokenizer;
import java.util.PriorityQueue;
public class DijkstraTest {
static class Node {
int vertex, weight;
Node next;
public Node(int vertex, int weight, Node next) {
super();
this.vertex = vertex;
this.weight = weight;
this.next = next;
}
@Override
public String toString(){
return "Node [vertex=" + vertex + ", weight=" + weight + ", next=" + next + "]";
}
}
static class Vertex implements Comparable<Vertex> {
int to, weight;
public Vertex(int to, int weight) {
super();
this.to = to;
this.weight = weight;
}
@Override
public int compareTo(Vertex o){
return Integer.compare(this.weight, o.weight);
}
}
public static void main(String[] args) throws Exception {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st = new StringTokenizer(br.readLine());
int V = Integer.parseInt(st.nextToken());
int E = Integer.parseInt(st.nextToken());
st = new StringTokenizer(br.readLine());
int start = Integer.parseInt(st.nextToken());
int end = Integer.parseInt(st.nextToken());
final int INF = Integer.MAX_VALUE;
Node[] adjList = new Node[V];
int[] minDistance = new int[V];
boolean[] vis = new boolean[V];
int from, to, weight;
for(int i=0; i<E; i++){
st = new StringTokenizer(br.readLine());
from = Integer.parseInt(st.nextToken());
to = Integer.parseInt(st.nextToken());
weight = Integer.parseInt(st.nextToken());
adjList[from] = new Node(to, weight, adjList[from]);
}
PriorityQueue<Vertex> pq = new PriorityQueue<>();
Arrays.fill(minDistance, INF); // 최소값 갱신 위해서 MAX로 초기화
minDistance[start] = 0;
pq.offer(new Vertex(start, minDistance[start])); // 시작점
Vertex minVertex;
while(!pq.isEmpty()){
// step1. 미방문 정점 중 출발지에서 가장 가까운 정점 선택
minVertex = pq.poll();
if(vis[minVertex.to]) continue; // 이미 최소 비용이 확정된 정점은 패스
minDistance[minVertex.to] = minVertex.weight;
vis[minVertex.to] = true;
if(minVertex.to == end) break; // 목적지 도착
// step2. 미방문 정점들에 대하여 선택된 경유지를 거쳐서 가는 비용과 기존 최소 비용을 비교하여 업데이트
for(Node tmp = adjList[minVertex.to]; tmp != null; tmp = tmp.next){
if(vis[tmp.vertex]) continue;
if(minDistance[tmp.vertex] > minDistance[minVertex.to] + tmp.weight){ // 시작점에서 부터 최저 비용 갱신
minDistance[tmp.vertex] = minDistance[minVertex.to] + tmp.weight;
pq.offer(new Vertex(tmp.vertex, minDistance[tmp.vertex])); // 갱신된 최소 비용 정보 삽입
}
}
//System.out.println(Arrays.toString(minDistance));
}
System.out.println(minDistance[end] != INF ? minDistance[end] : -1);
br.close();
}
}if(minDistance[tmp.vertex] > minDistance[minVertex.to] + tmp.weight){
: 기존의 최소 비용보다 크면 해당 경로를 고려 대상에서 제외한다.
: 이 부분이 Dijkstra가 그리디 알고리즘인 이유다. (없으면 완탐이 된다.)
3. 정리
| 알고리즘 | 용도 | 설명 | 표현 | 시간복잡도 | 기타 |
| Prim | 최소 신장 트리 | 가중치가 있는 무방향 그래프에서 최소 신장 트리를 찾는 알고리즘. | 인접 리스트, 인접 행렬 | FOR : O(V^2) PQ : O(ElogE) |
무방향 |
| Kruskal | 최소 신장 트리 | 가중치가 있는 무방향 그래프에서 최소 신장 트리를 찾는 알고리즘. | 간선 리스트 | O(ElogE + V) | 무방향 |
| Dijkstra | 최소 경로 | 음의 가중치가 없는 그래프의 한 정점에서 다른 정점들까지의 최단 거리 비용을 구하는 알고리즘. | 인접 리스트, 인접 행렬 | FOR : O(V^2) PQ : O(ElogE) |
음의 가중치 X |
| Bellman-Ford | 최소 경로 | 그래프의 한 정점에서 다른 정점들까지의 최단 거리 비용을 구하는 알고리즘. | 간선 리스트 | O(VE) | 음의 가중치 O |
| Floyd-Warshall | 최소 경로 | 모든 정점 사이의 최단 거리 비용을 구하는 알고리즘. | 인접 행렬 | O(V^3) | 음의 가중치 O 단, 음수 사이클 X |
'Algorithm > with Java' 카테고리의 다른 글
| [Java] DP - 응용 (0) | 2024.03.02 |
|---|---|
| [Java] Memoization, DP (0) | 2024.03.02 |
| [알고리즘] 17281. 야구 (0) | 2024.02.26 |
| [알고리즘] 3124. 최소 스패팅 트리 (0) | 2024.02.26 |
| [알고리즘] 1251. 하나로 (0) | 2024.02.26 |