[Java] Memoization, DP
2024. 3. 2. 15:56ㆍAlgorithm/with Java
1. Memoization
가. 피보나치수열
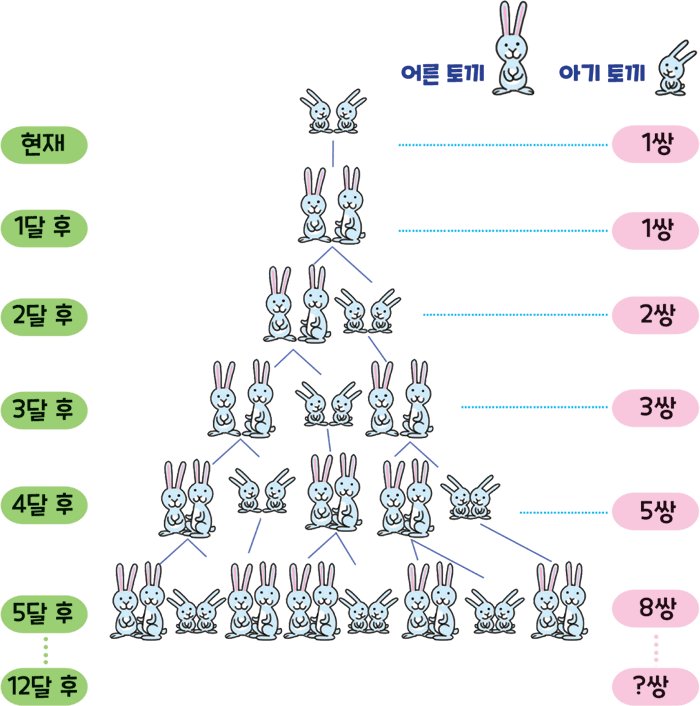
F0 = 0;
F1 = 1;
Fn+2 = Fn+1 + Fn;피보나치수열의 점화식이다.
fib(n)
IF m < 2 : RETURN n
ELSE : RETURN fibo(n - 1) + fibo(n - 2)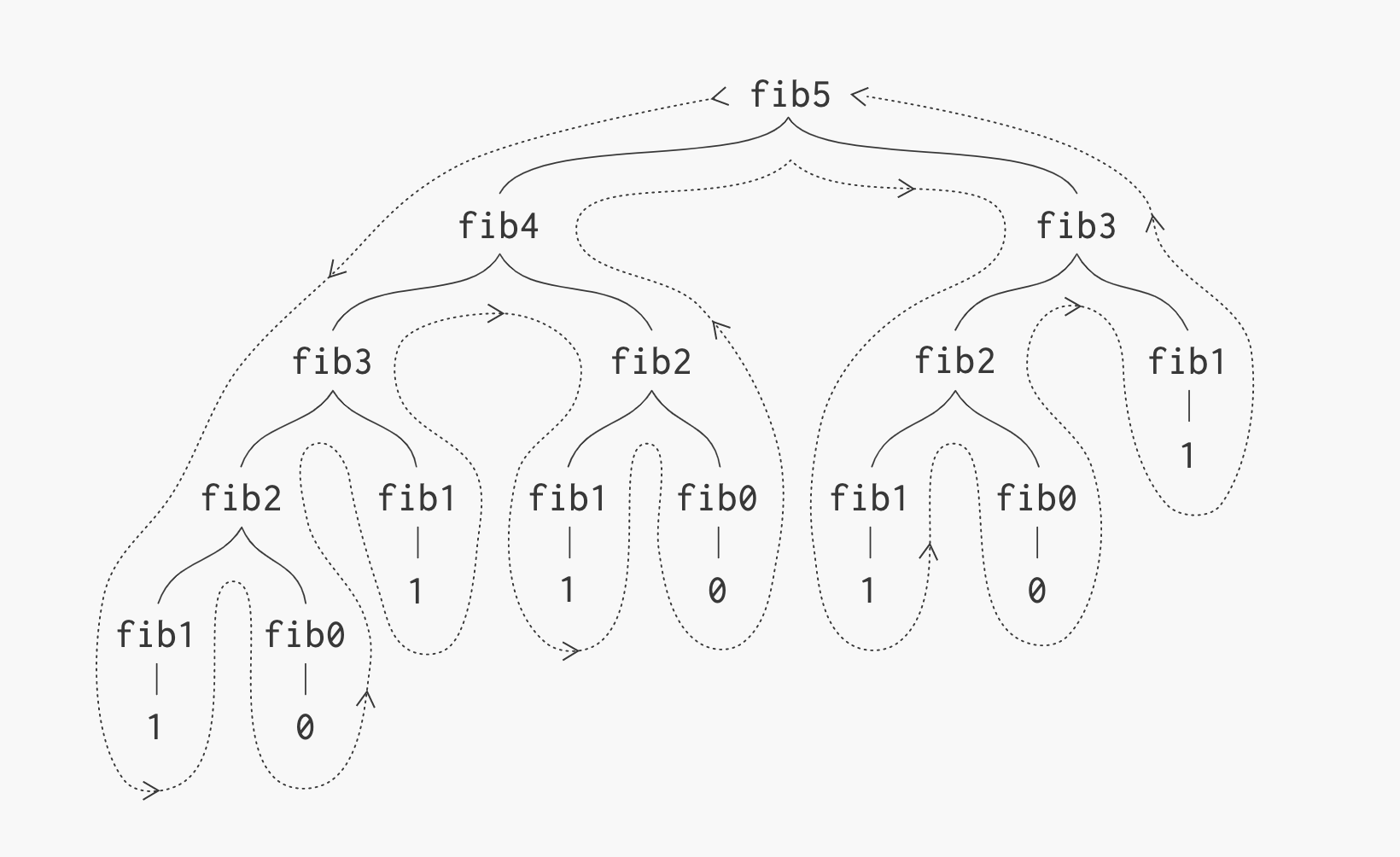
fib1, fib2 ... 등이 중복 호출이 발생한다.
fib()는 순수 함수다.
그렇기 때문에 fib1, fib2, … 등을 계산 결과는 항상 일정하다.
한 번만 계산하고 결괏값을 재사용할 수 있다.
나. Memoization
- 컴퓨터 프로그램을 실행할 때 이전에 계산한 값을 메모리에 저장하여 매번 다시 계산하지 않도록 하여 전체적인 실행속도를 빠르게 하는 기술
memo[0] = 0;
memo[1] = 1;
fib(n)
IF n >= 2 AND memo[n] = 0
memo[n] <- fib(n-1) + fib(n-2)
RETURN memo[n]import java.util.Scanner;
public class FibonacciTest {
static long callCnt1, callCnt2;
static long[] memo;
static long fibo1(int n) {
callCnt1++;
if(n<2) return n;
return fibo1(n-1) + fibo1(n-2);
}
static long fibo2(int n) {
callCnt2++;
if(n >= 2 && memo[n]==0) memo[n] = fibo2(n-1) + fibo2(n-2);
return memo[n];
}
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int N = sc.nextInt();
memo = new long[N+1];
memo[0] = 0;
memo[1] = 1;
System.out.println(fibo1(N));
System.out.println(callCnt1);
System.out.println("---------------");
System.out.println(fibo2(N));
System.out.println(callCnt2);
}
}
/*
45
1134903170
3672623805
---------------
1134903170
89
*/
하지만 이 방식은 memo라는 추가적인 메모리 공간이 필요하다.
재귀 함수 호출과 memo 저장을 위해서는 많은 메모리를 사용한다.
이는 실행 속도 저하 또는 메모리 부족을 발생시킬 수 있으므로 주의하자.
2. DP
- 동적 계획법
- 최적화 문제를 해결하는 알고리즘이다.
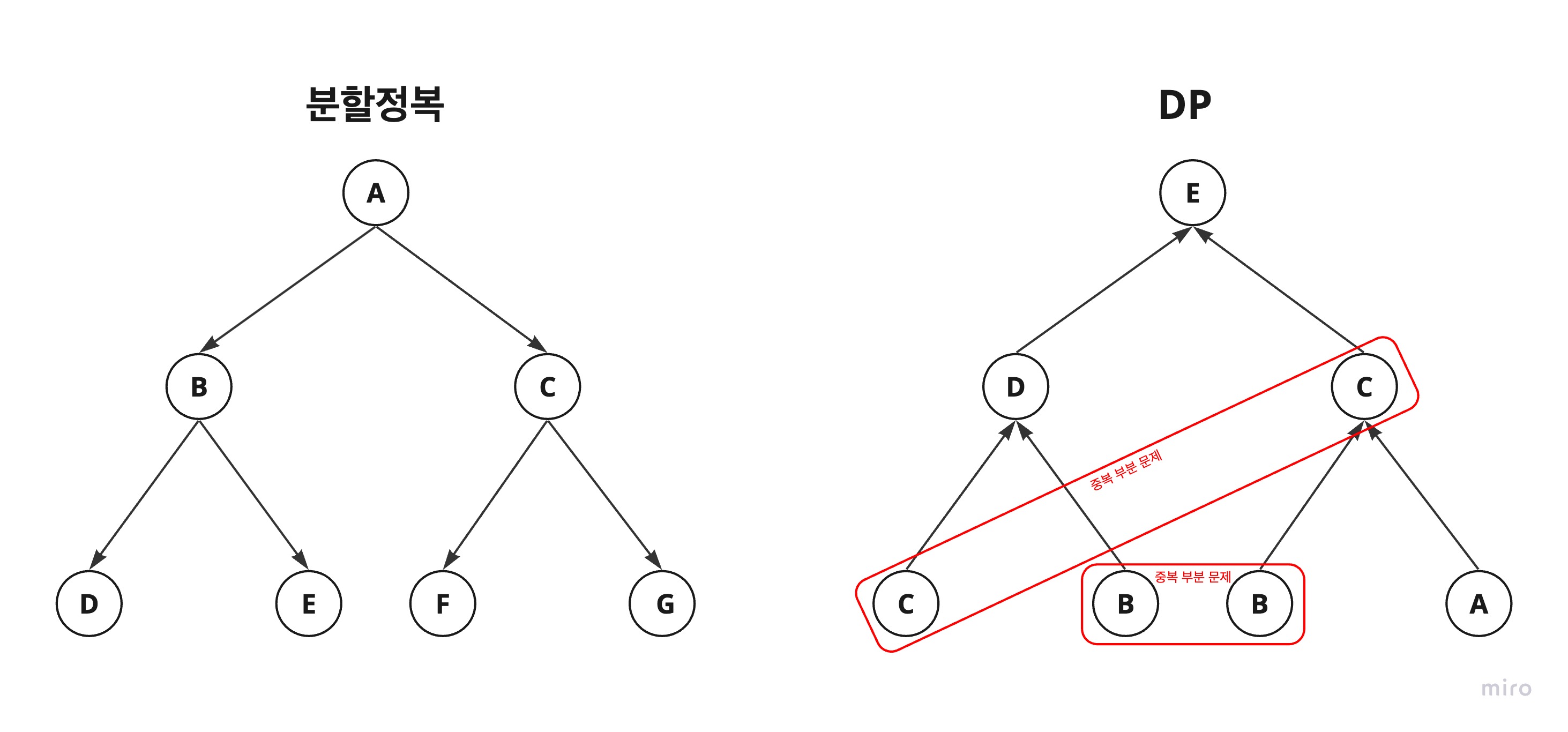
- 먼저 작은 부분 문제들의 해들을 구하고 이들을 이용하여 큰 크기의 부분 문제들을 해결하여, 최종적으로 원래 주어진 문제를 해결하는 알고리즘 설계 기법이다. (분할 정복?)
가. DP의 적용 요건
DP로 풀어내기 위해서는 2가지 조건을 만족해야 한다.
- 중복 부분문제 구조
: 전체 문제를 분할하는 과정에서 같은 부분 문제가 반복적으로 나타나는 특성 - 최적 부분문제 구조
: 부분 문제의 최적이 모여서 전체 문제의 최적을 이룬다.
나. DP? 분할 정복?
| 동적 계획법 | 분할 정복 | |
| 최적 부분 문제 | O | O |
| 중복 부분 문제 | O | X |
| 메모이제이션 | O | X |
| 접근 방법 | 상향식, 하향식 | 하향식 |
다. DP 접근 방법
| 하향식 | 상향식 | |
| 설명 | 큰 문제 해결을 위해서 작은 문제 호출 | 작은 문제 해결 후 큰 문제 해결 |
| 구현 | 재귀 함수 | 반복문 |
| 결과 저장 | 계산한 결과를 반드시 사용. | 계산한 결과를 담아놓기만 하고 사용하지 않을 수 있다. |
| 특징 | 점화식을 이해하기 쉬움. | 재귀 호출이 없어 시간과 메모리 사용량이 감소. |
보통 DP는 상향식 접근법을 더 많이 사용한다.
라. 피보나치 DP로 구현
import java.util.Scanner;
public class FibonacciTest {
static long[] dp;
static long fiboDP(int n) {
dp[0] = 0;
dp[1] = 1;
for (int i = 2; i <= n; i++) {
dp[i] = dp[i-1] + dp[i-2];
}
return dp[n];
}
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int N = sc.nextInt();
dp = new long[N+1];
System.out.println(fiboDP(N));
}
}
'Algorithm > with Java' 카테고리의 다른 글
| [알고리즘] 1753. 최단경로 (0) | 2024.03.02 |
|---|---|
| [Java] DP - 응용 (0) | 2024.03.02 |
| [Java] 최단 경로 (0) | 2024.02.27 |
| [알고리즘] 17281. 야구 (0) | 2024.02.26 |
| [알고리즘] 3124. 최소 스패팅 트리 (0) | 2024.02.26 |