2022. 10. 13. 00:16ㆍ학부 강의/AI 입문
1. 다층 신경망 (FNN)
2 계층으로 구성된 다층 퍼셉트론(MLP)은 XOR 기능을 구현해냈다.
이로써 퍼셉트론의 선형 분리성의 한계를 극복했다.
오류 역전파 알고리즘(Backpropagation)으로 다 계층 구조 활용의 최대 걸림돌인 학습 문제를 해결했다.
활성화 함수로 비선형 활성화 함수(시그모이드 함수)를 적용하면서 다양한 함수 기능 구현.
시그모이드 함수를 사용하는 순간부턴 다층 퍼셉트론보단 다층 신경망, 일반 신경망(FNN)이라 칭한다.
선형/비선형 회귀, 이진 분류, 다중 분류 등에 활용된다.
가. FNN 구조
- Feed forward 구조
- 한 개의 히든 계층
- 다양한 활성화 함수 사용
- 일반적으로 완전연결층(fully-connected)
보통 ‘계층’이라 함은 앞 단 계층과의 가중치까지 포함한다는 의미다.
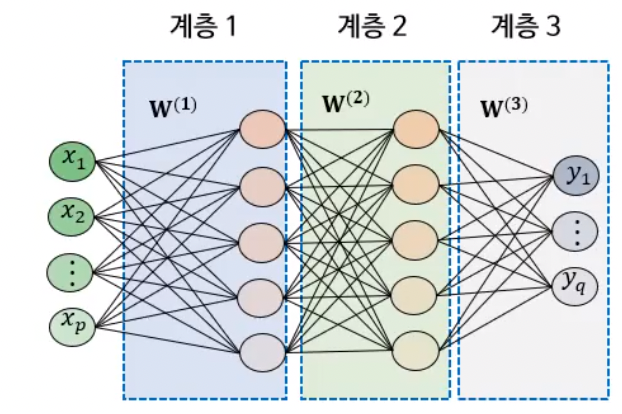
나. FNN 동작
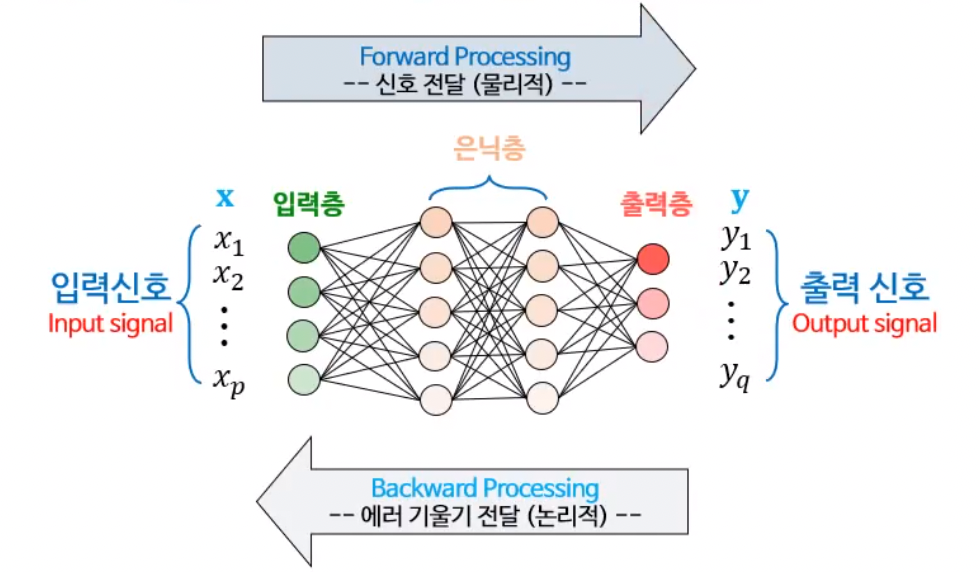
- 순방향 처리 : 추론
- 역방향 처리 : 학습을 위한 backpropagation 알고리즘 수행
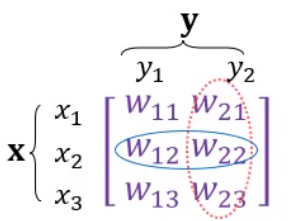
다. 가중치 행렬 표기 방식
 |
 |
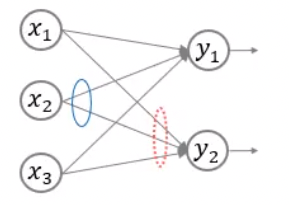 |
가중치는 행렬을 이용해서 표기한다.
하나의 입력 노드에서 뻗어나가는 가중치는 행열의 행에 해당한다.
하나의 출력 노드에 연결되는 가중치는 행열의 열에 해당한다.
2. FNN의 계층
가. 행렬곱

참고하세요.
행렬 곱셈 - 위키백과, 우리 모두의 백과사전
위키백과, 우리 모두의 백과사전. 행렬 곱셈을 위해선 첫째 행렬의 열 갯수와 둘째 행렬의 행 갯수가 동일해야한다. 곱셈의 결과 새롭게 만들어진 행렬은 첫째 행렬의 행 갯수와 둘째 행렬의 열
ko.wikipedia.org
나. 뉴럴 계층
(1) 어파인 계층 (Affine)
An affine layer, or fully connected layer, is a layer of an artificial neural network
in which all contained nodes connect to all nodes of the subsequent layer.
Affine 계층이란 Neural Network에서 fully-connected layer를 의미한다.
완전 연결 계층에 의한 변환은 기본적으로 '선형' 변환이다. (xW + b → y)
그래서 선형 (linear) 계층이라고도 한다.
그리고 여기에 '비선형' 효과를 부여하는 것이 활성화 함수이다.
출처 : https://deepai.org/machine-learning-glossary-and-terms/affine-layer
출처 : https://yxxshin.github.io/2022/08/07/2022-08-07-Affine-Layer-Backprop/
출처 : https://dltpgh7060.tistory.com/66
(2) 비선형 계층
비선형 활성화 함수를 사용하는 뉴런으로 구성된 계층
ex) 시그모이드, ReLU …
(3) 소프트맥스 계층

입력 벡터를 확률로 변환하는 기능을 가지고 있다.
필요시 출력 단에 사용한다.
확률의 특성상 모든 출력 값의 합은 1이 된다.
3. 순방향 처리 (추론)
가. 순방향 처리
신경망의 태스크(회귀, 분류 등)를 수행한다.
순방향 처리의 실제 구현에 있어 단위 데이터별 처리 (단일 모드 or 샘플 모드)와 여러 데이터를 한 번에 처리하는 배치 모드 방식을 사용함.
(1) 단일 모드
한번에 한 개의 입력을 처리.

(2) 배치 모드
한번에 여러 개의 입력(batch)을 처리.

4. 파이썬 실습
가. 파이썬 라이브러리
(1) numpy
NumPy는 행렬이나 일반적으로 대규모 다차원 배열을 쉽게 처리할 수 있도록 지원하는 파이썬의 라이브러리이다.
NumPy는 데이터 구조 외에도 수치 계산을 위해 효율적으로 구현된 기능을 제공한다.
- import
import numpy as np
- 1차원 배열 생성
x = np.array([0, 10, 20, 30, 40, 50])
- 2차원 배열 생성
y = np.array([[0, 1, 2],
[10, 11, 12]])# 기존 배열의 형상의 초기화 배열 생성
z = np.zeros_like(y)
print(z)
- 배열 간 산술 연산과 내적
X = np.array([[1, 2],
[3, 4]])
Y = np.array([[3, 0],
[0, 6]])
X + Y
# array([[ 4, 2],
# [ 3, 10]])
X * Y
# array([[ 3, 0],
# [ 0, 24]])
np.dot(X, Y)
# array([[ 3, 12],
# [ 9, 24]])
- 내적
X = np.array([1, 2, 3])
Y = np.array([1, 2, 3])
np.dot(X, Y)
# 14
- 행열곱
#행렬곱 사례 2 : 3x2 행렬 * 2x3 행렬
X = np.array([[11, 21, 31],
[42, 5, 6]])
Y = np.array([[1, 2],
[2, 31],
[13, 14]])
np.dot(X, Y)
(2) matplotlib
Matplotlib는 Python 프로그래밍 언어 및 NumPy 라이브러리를 활용한 시각화(plot) 라이브러리다.
# matplot library
import matplotlib.pyplot as plt
- 그래프 1
plt.figure(figsize=(8,4))
x = [10, 20, 30, 40]
y = [1, 4, 9, 16]
plt.plot(x, y, "b--")
plt.plot(x, y, "r^")
plt.grid(True, ls="--", lw=1)
plt.show()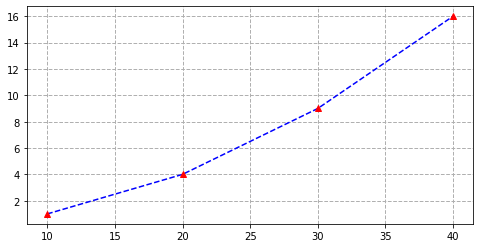
- 그래프 2
plt.figure(figsize=(8,4))
x = [10, 20, 30, 40]
y = [1, 4, 9, 16]
plt.plot(x, y, c="b", lw=2, ls=":", ms=15, marker="o", mew=5, mec="g", mfc="r")
plt.grid(True, ls="--", lw=1)
plt.show()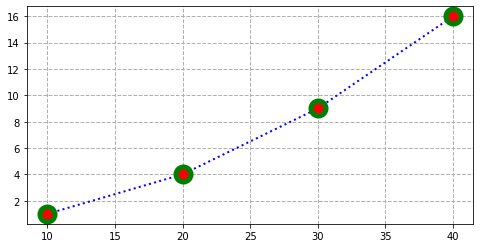
- 활성화 함수
def sigmoid(x):
return 1 / (1 + np.exp(-x))
def tanh(x):
return (np.exp(x)- np.exp(-x)) / (np.exp(x) + np.exp(-x))
def relu(x):
return np.maximum(0, x)
x = np.arange(-4.1, 4.1, 0.1)
plt.plot(x, sigmoid(x), '-', label="Logistic sigmoid")
plt.plot(x, tanh(x), '--', label="Hyperbolic tangent")
plt.plot(x, relu(x), ':', label="ReLU")
plt.plot(0, sigmoid(0), 0, tanh(0), "ko") # x = 0일 때의 함수값 표시
plt.title("Activation functions")
plt.ylim(-1.5, 2.1)
plt.grid(color='#BDBDBD', linestyle='-', linewidth=0.5)
plt.legend()
plt.show()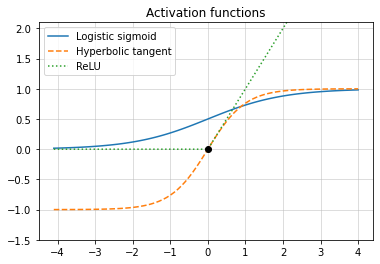
나. 신경망 구현

def sigmoid(x):
return 1 / (1 + np.exp(-x))
def softmax(x):
max = np.max(x)
exp_x = np.exp(x - max) # overflow를 방지
sum_exp_x = np.sum(exp_x)
y = exp_x / sum_exp_x
return y
# 소프트맥스 계층을 구현하는 방법인 것 같은데 자세히 다루지 않겠다. (모른다 헤헷)np.max(x): 단일 array x 내에서 최댓값 반환np.exp(x): 밑이 자연상수 e인 지수함수(e^x)로 변환
## 1. Setting the weight of 2-layer neural network
W1 = np.array([[0.4, 0.2, 0.3], [0.1, 0.2, 0.1]])
b1 = np.array([0.1, 0.2, 0.2])
W2 = np.array([[0.1, 0.4], [0.2, 0.3], [0.4, 0.6]])
b2 = np.array([0.2, 0.1])
## 2. Perform inference for an input patten
x = np.array([2.2, 1.3]) # 입력 샘플
# 계층 1 연산
v1 = np.dot(x, W1) + b1
h1 = sigmoid(v1)
print("v1:", v1), print("h1:", h1)
# 계층 2 연산
v2 = np.dot(h1, W2) + b2
h2 = sigmoid(v2)
print("v2:", v2), print("h2:", h2)
# 2.3 소프트맥스함수 적용
y = softmax(h2)
print("입력 : ", x)
print("출력 : ", y)# 결과
v1: [1.11 0.9 0.99]
h1: [0.75212911 0.7109495 0.72908792]
v2: [0.70903798 1.05158925]
h2: [0.67018855 0.74107996]
입력 : [2.2 1.3]
출력 : [0.48228457 0.51771543]
'학부 강의 > AI 입문' 카테고리의 다른 글
| 2022-11-07 AI입문_8 (0) | 2022.11.08 |
|---|---|
| 2022-11-05 AI입문_7 (0) | 2022.11.06 |
| 2022-10-05 AI입문_5 (0) | 2022.10.05 |
| 2022-09-28 AI입문_4 (0) | 2022.09.29 |
| 2022-09-20 AI입문_3 (1) | 2022.09.20 |