2022. 11. 6. 00:11ㆍ학부 강의/AI 입문
1. 기울기 강하 기법
가. 학습법 개관
(1) 신경망 학습법 개관
- 분석적 기법 : 방적식을 구한 후 해를 계산하는 방식
→ 계산이 복잡하고 비가역적이면 계산이 불가하다.
- 에러 정정 학습법 : 오차를 점직적으로 줄여가는 방식

(2) 에러 정정 기법

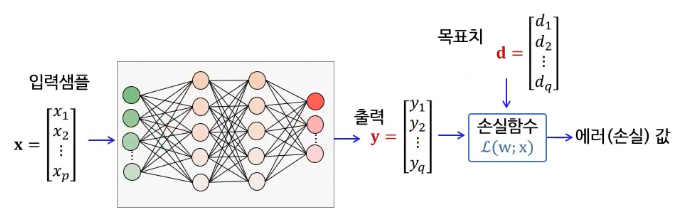
주어진 입력 샘플에 대해 출력을 산출한다.
이후 출력과 목표 출력 간의 차이가 줄어들도록 가중치를 변경한다.
- 손실(Loss, 에러)를 어떻게 계산할 것인가? → 손실 함수로 정량화
- 손실이 줄어들도록 가중치를 조정하는 방법 → 기울기 강하 기법 활용
나. 손실함수
(1) 손실 함수
손실 함수는 목표치와 실제 출력 간의 차이(손실, 에러)를 계량화하는 함수.
에러 함수의 종류는 다양한다. ex) 평균제곱에러, 교차엔트로피 에러 등
(2) 평균제곱에러
평균 제곱 에러는 영어로 MSE(Mean Square Error)다.
출력 값과 목표치의 값의 제곱에 1/2를 곱한 값 : 1/2 x (목표치 - 출력값)^2
다. 기울기 강하 기법
(1) 기울기 강하 기법
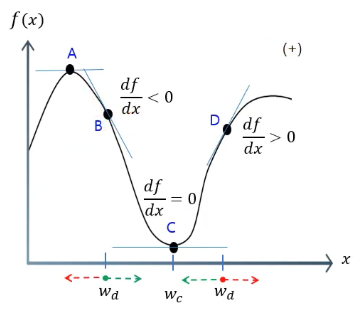
우리는 함수의 접선의 기울기를 안다면 최소 또는 최댓값(변곡점)의 방향을 알 수 있다.
그리고 접선의 기울기는 미분하면 구할 수 있다.
기울기 강하 기법은 손실 함수의 접선 기울기를 이용해서 손실함수가 최소값을 가지도록 반복적으로 가중치를 조정해 나간다.

구체적으로 가중치를 조정하는 방식을 알아보자면 기존의 가중치에 기울기를 빼면 점차 손실함수의 값이 최소가 되는 지점에 근접할 수 있게 된다.
한 번에 조정되는 가중치 크기를 적절하게 조절하기 위해서 갱신률을 곱한다.
(2) 기울기 강하 기법의 한계
이 녀석이 가끔 멍청하게도 전역 최소점(global minima) 대신에 국소 최소점 (local minima)에 꽂히는 경우가 있다.

이미지 출처 : https://ko.wikipedia.org/wiki/극값
2. 단계층 신경망 학습 : 델타 규칙
델타 규칙(Delta rule)은 Window & Hoff 학습법이라고도 한다.
단층 신경망에 대한 기울기 강하 학습법이며 손실 함수로 평균 제곱 에러(MSE)를 사용한다.
델타 규칙의 구체적인 손실 함수의 수식표현과 가중치에 대한 손실함수의 편미분은 다루지 않겠다.
이는 앞에서 살펴본 가중치 강하 기법의 연장선 상에 있다.
앞의 내용을 충분히 이해할 수 있다면 금방 다시 배울 수 있을 것이다.
3. 다계층 신경망 학습 : 역전파 학습 알고리즘
오류 역전파 알고리즘, 역전파 알고리즘, 역전파 학습 알고리즘, 백프로퍼게이션 모두 같은 것이다.
퍼셉트론의 한계를 넘어설 하나의 가능성으로 다층 신경망이 주목받았다.
하지만, 다층 신경망은 학습에 있어서 문제가 있었다.
델타 규칙은 단층 신경망에서만 유효하게 동작했다.
백프로퍼게이션 알고리즘은 다층 신경망의 학습을 가능하게 했다.
다층 신경망의 실용적인 활용의 가능성을 열어 신경망의 부활을 가져왔다.
하지만, 기울기 소실 또는 폭증(error gradient vanishing or explosion) 현상으로 계층의 개수가 커지면 실용성이 저하되는 문제가 있다.
이에 다층 신경망은 소규모 응용에만 사용된다.
가. 역전파 학습 개념
결국에 신경망의 학습에 있어서 중요한 것은 가중치를 조정하는 것이다.
다층 신경망의 특성상 노드와 가중치 역시 복수의 계층으로 구성된다.
그렇기에 출력 계층에서 출력 값과 목표 출력 간의 오차를 계산하고 이를 이용해 앞선 은닉층의 가중치를 적절하게 조정할 필요가 있다.
이때 출력층의 오차가 은닉층으로 전파되는 순서는 입력과 출력의 역순으로 진행된다.
역전파 알고리즘은 가중치를 조정하기 위해서 가중치 에러 기울기라는 것을 계산한다.
다시 가중치 에러 기울기를 계산하기 위해서 노드 에러 기울기를 계산한다.
출력층 에러 → 노드 에러 기울기 → 가중치 에러 기울기 → 앞단 노드의 에러 기울기 → 앞단 가중치 에러 기울기 → 앞 앞단 노드의 에러 기울기 → 앞앞단 가중치 에러 기울기 → … → 반복 → … → 완료

아래에서는 노드 에러 기울기와 가중치 에러 기울기를 구하는 방법에 대하여 알아보고 가중치를 조정하는 방법과 사례를 정리해보자.
나. 합성함수의 미분
에러 기울기를 구하기 위해서 합성함수의 미분법을 알고 있어야 한다.
g(f(x))의 미분은 g’(f(x))f’(x)다.
예를 들어 y=(3x+1)^2를 미분하면 …
g’(f(x)) = 2(3x+1)이고 f’(x) = 3이다.
고로 최종적으로 3 * 2(3x+1) = 6(3x+1)로 미분된다.
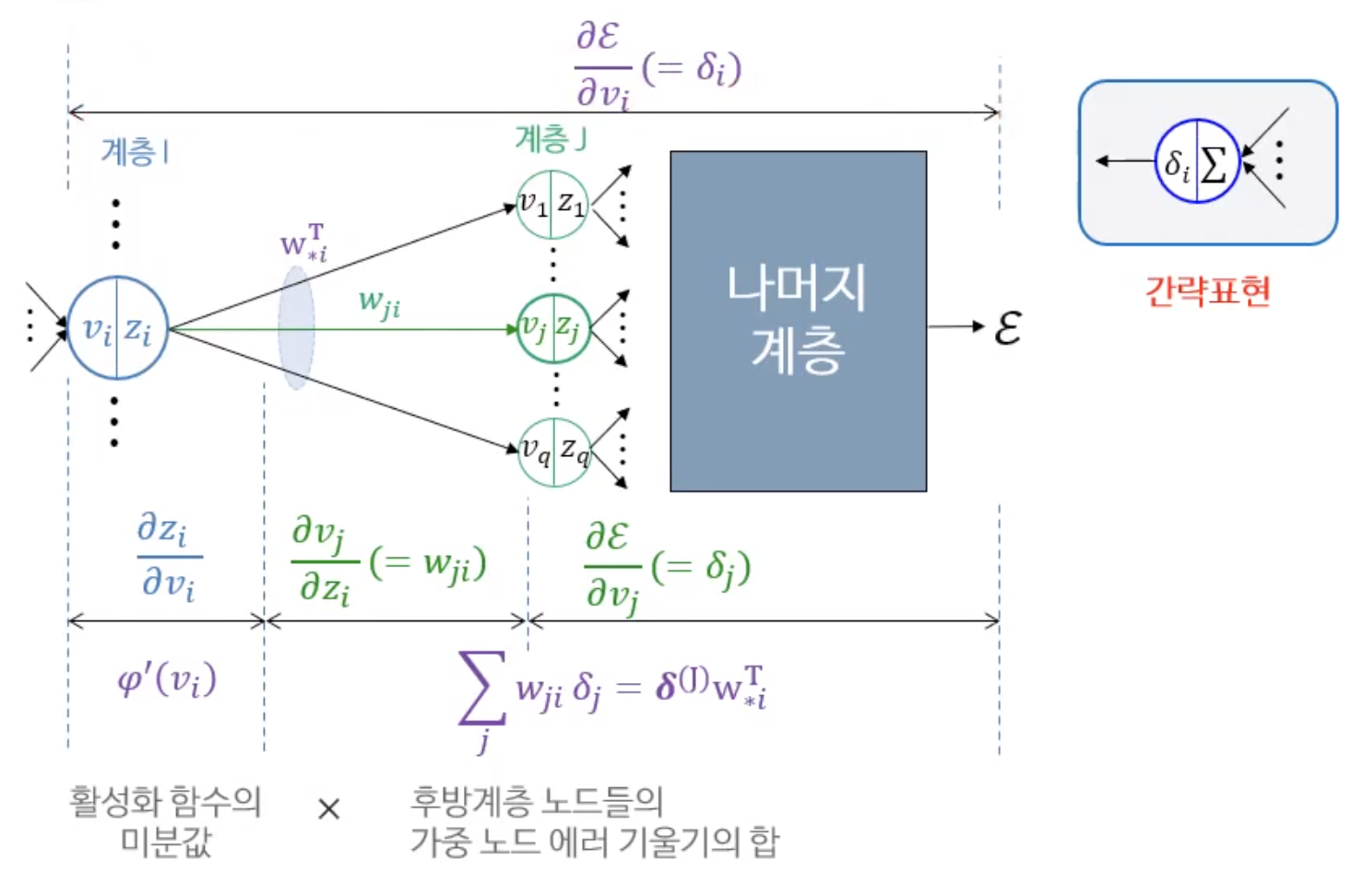
다. 노드 에러 기울기
노드의 에러 기울기는 노드의 가중입력합에 대한 에러 함수의 접선 기울기(편미분)다.
노드 에러 기울기는 활성화 함수의 미분 값과 후방 계층 노드의 가중 노드 에러 기울기 합을 곱하면 구할 수 있다.

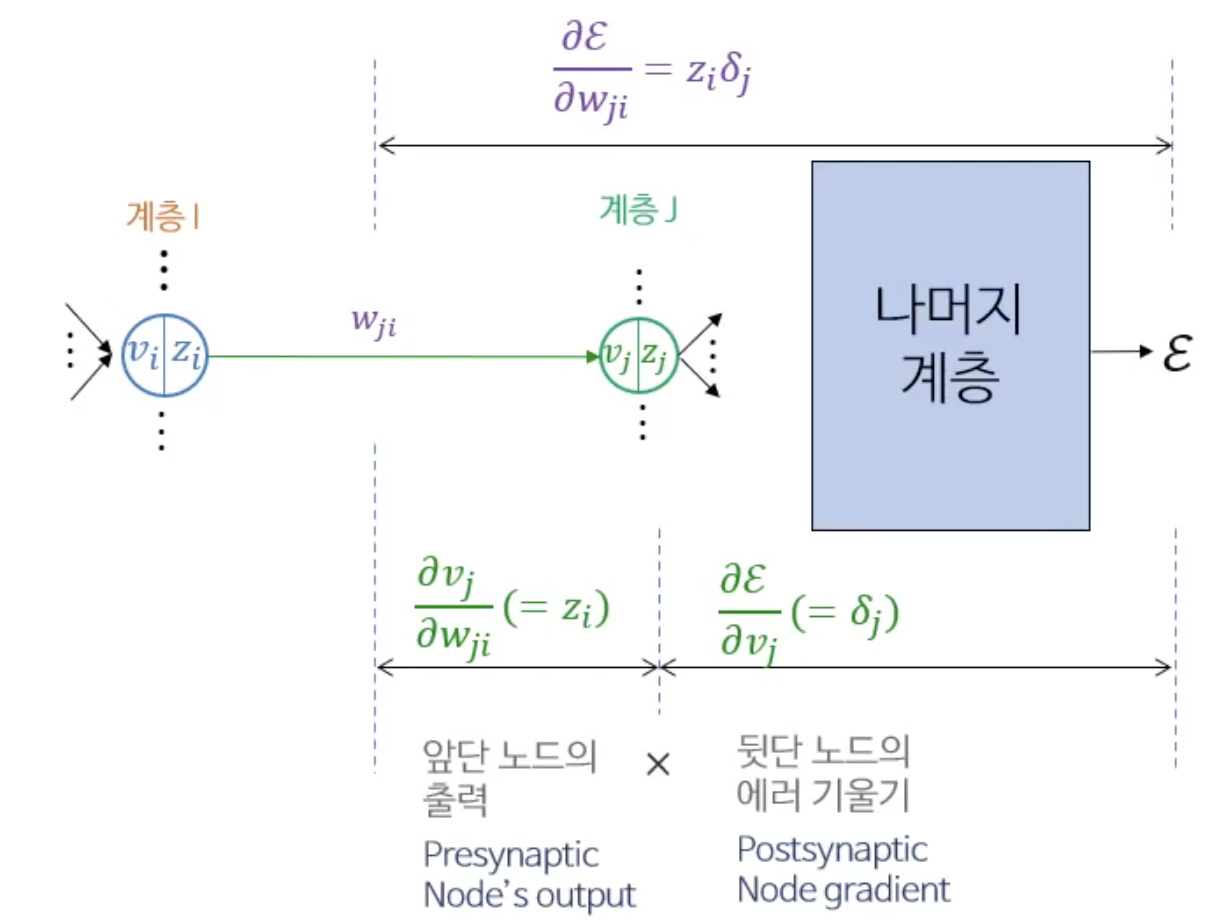
라. 가중치 에러 기울기
가중치 에러 기울기는 가중치에 대한 에러 함수의 접선 기울기(편미분)다.
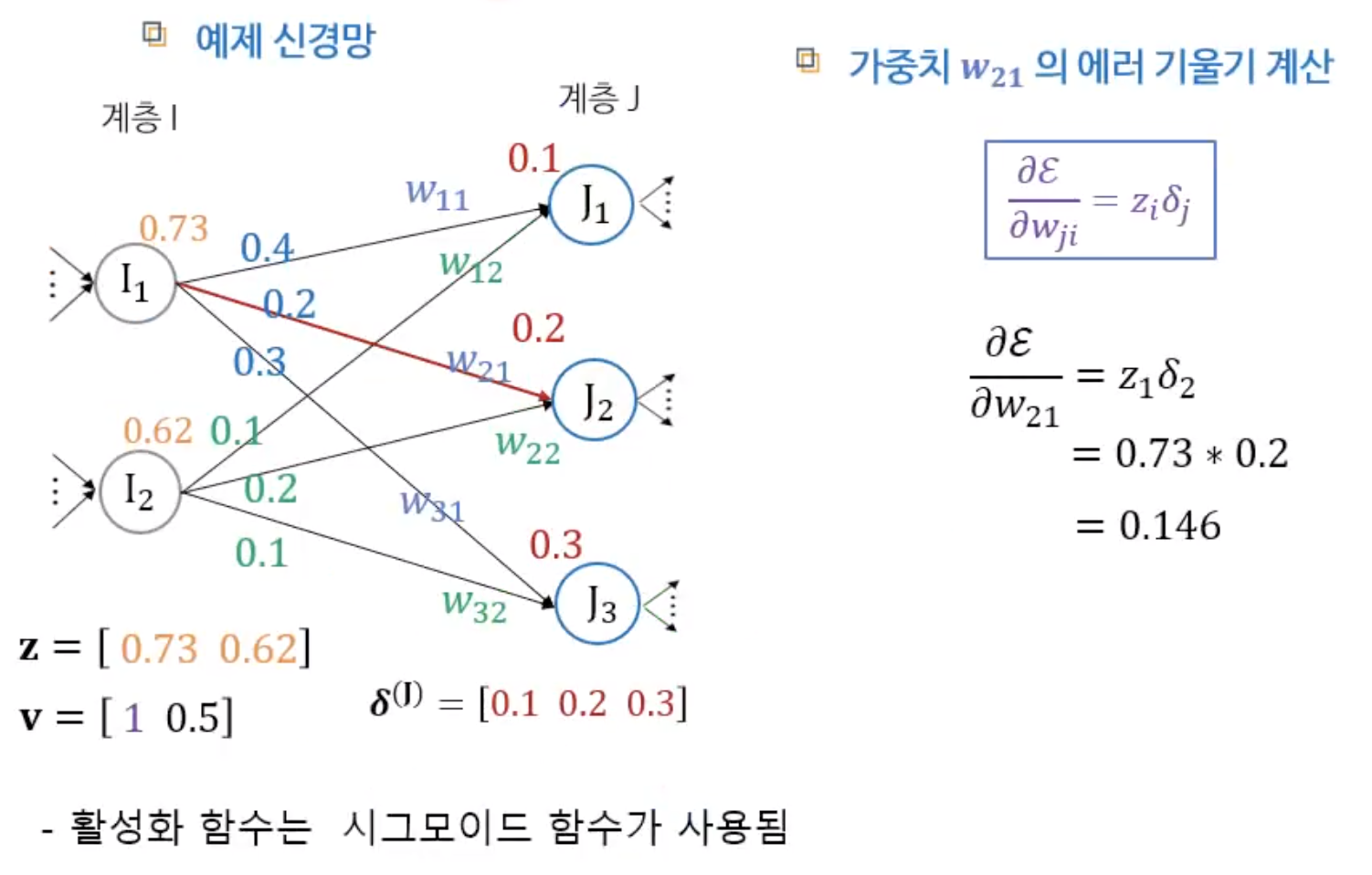
마. 가중치 갱신

기존 가중치에 가중치 에러 기울기와 학습률을 곱한 값을 뺀다.
중간고사 때문에 많이 밀렸다… 헉헉
'학부 강의 > AI 입문' 카테고리의 다른 글
| 2022-11-13 AI입문_9 (0) | 2022.11.13 |
|---|---|
| 2022-11-07 AI입문_8 (0) | 2022.11.08 |
| 2022-10-13 AI입문_6 (0) | 2022.10.13 |
| 2022-10-05 AI입문_5 (0) | 2022.10.05 |
| 2022-09-28 AI입문_4 (0) | 2022.09.29 |