2022. 11. 8. 00:09ㆍ학부 강의/AI 입문
1. 딥러닝 개요
가. 딥러닝의 등장과 확산
1) 딥러닝의 등장
다층 신경망은 계층의 개수가 커지면서 신경망의 학습이 제대로 이뤄지지 않는 문제가 있다.
기울기 소실과 기울기 폭증과 관련된 문제다.
심층 신경망 (deep neural network : deep learning)은 이러한 문제를 해결하면서 등장했다.
2006년 힌튼 (Hinton) 교수가 심층신경망의 학습 가능성을 제시했다.
이는 적층 RBM(Stack Restricted Bolzmann Manchin) 기반 가중치 학습, 심층신경망인 DBN, 사전학습(pretrain) 후 상세 조정(wake-sleep 알고리즘)과 같은 기술을 사용했다.
2) 딥러닝의 확산
딥러닝은 아래와 같은 배경에서 활성화되었다.
- 혁신 알고리즘
- 공개 개발환경
- 고성능 컴퓨팅환경 (GPU, 클라우드)
- 풍부한 대규모 학습 데이터
본격적으로 딥러닝에 대한 관심이 커지면서 몇 가지 변화가 생겼다.
- 오래전에 개발된 딥러닝 모델를 활용하고자 시도하기 시작했다. CNN과 LSTM 등 그간 효과적인 학습 방법의 부재로 사장되었던 모델들이 재평가되기 시작함.
- 안정적인 학습을 위한 다양한 기법 및 알고리즘, 아키텍처 지원 기술 개발이 가속화되었다.
- 대규모 데이터셋 개발 착수
- GPU 등 대규모 학습에 필요한 컴퓨팅 환경에 대해서 모각하기 시작.
- 다양한 응용의 딥러닝 모델 탐구
나. 딥러닝 개요
딥러닝은 다층 구조의 신경망으로서 많은 추출 특징의 수와 계층적 추상화 학습이 특징이다.
1) 딥러닝의 장점 : End-to-End 학습
Raw data 입력에서 특징을 사람의 개입 없이 자동으로 추출할 수 있다.
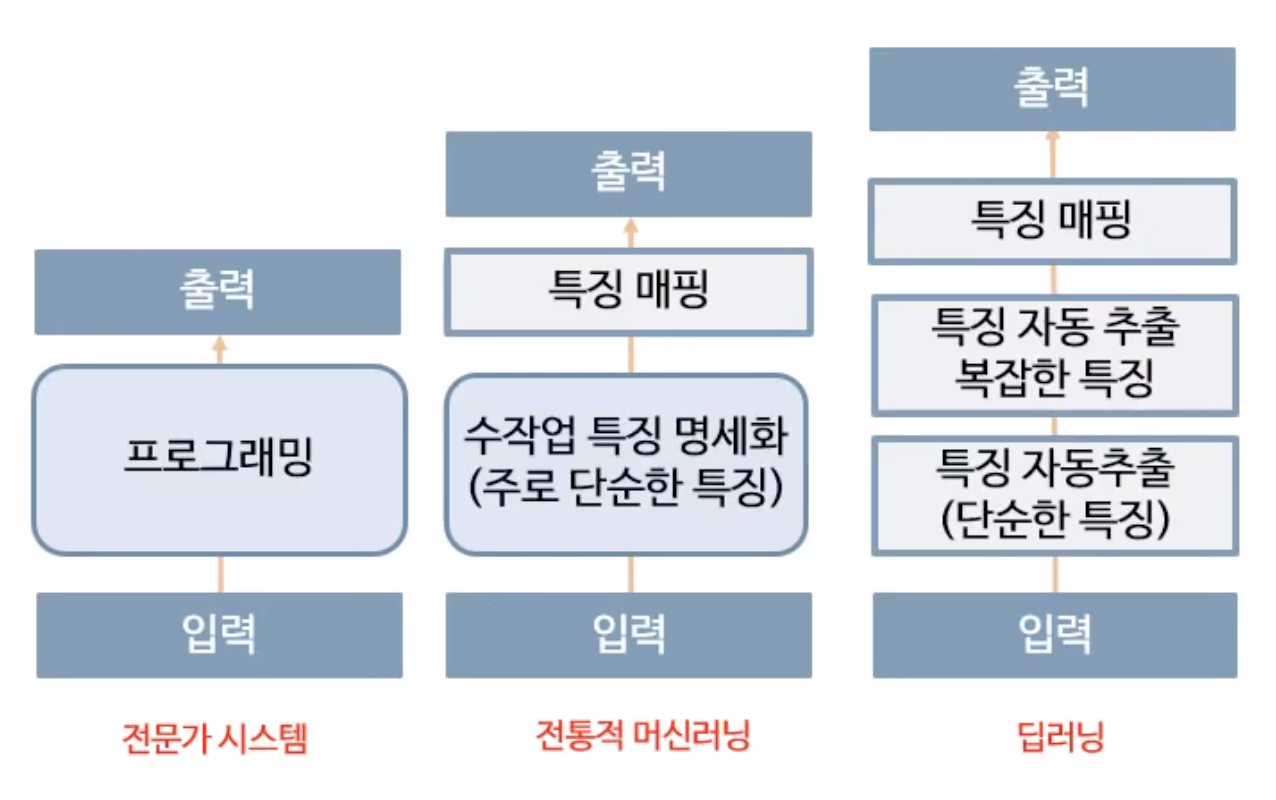
2) 초기 딥러닝의 기반 모델
초기 딥러닝은 컨볼루션망, 순환망 그리고 볼츠만 머신 계열망 등과 같은 다양한 망구조를 조합하여 활용했었다.
현재는 컴볼루션망과 순환망이 가장 흔하게 사용된다.
- 컨볼류션망(Convolutional)
- 주로 컴퓨터 비전에서 사용됨
- 여러 노드가 가중치 공유를 통한 계산량 축소
- 위치와 위상적 특징 추출 효율화
- 서브 샘플링으로 공산 축소
- 순환망 (Recurrent)
- 자연어 처리 등 시계열 데이터 처리에 유용함
- 노드의 출력 값, 상태 값을 되돌려 입력으로 사용
- 일종의 상태(메모리) 유지 효과
- RNN과 개선 모델인 LSTM
2. 컴퓨터 비전
가. 컴퓨터 비전 개요
컴퓨터 비전은 컴퓨터 SW와 HW를 이용해서 인간의 시작적인 인식 기능을 모사하는 것을 목표로 한다.
2차원 영상으로부터 3차원의 장면을 재구성하고, 해석하고, 이해하는 것을 연구하는 분야다.
Raw data → 전처리 → 특징 추출 → 장면 분석 → 묘사 (해석, 분류, 상황)
영상처리, 패턴 인식, 컴퓨터 그래픽스 등에 활용된다. (손글씨, 지문, 얼굴, 의료 영상)
기존에도 전통적인 컴퓨터 비전은 존재했다.
하지만 2000년대 기술에는 한계가 있었다.
막대한 수작업을 요하는 작업이었다.
작음(noise) 제거, 대비(constrast) 개선, 회색화(gray-scale), 에지(edge) 추출, 윤곽선(contour) 추출, 관심 영역(region of interest), 영역 분할(segmentation) 등 …
나. 컴퓨터 비전 : 특징 추출과 필터
1) 이미지 표현
기본적으로 흑백으로만 표현되는 이미지는 0~255의 숫자로 구성된 2차원 배열이며 단일 채널이다.

칼라 영상은 RGB 3개 채널, 3차원 배열로 구성된다.
각 영상은 0~255의 숫자로 구성된 2차원 배열로 구성된다.
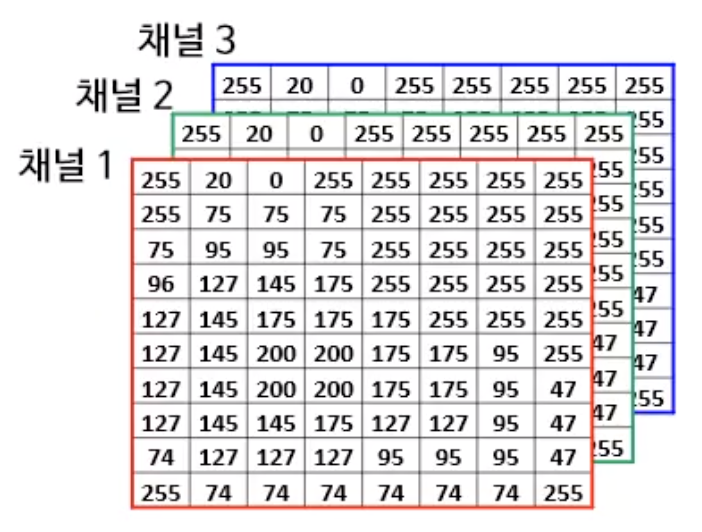
2) 필터
Linear filtering
- 연산 유형 : 교차 상관(cross-correlation), 합성곱(convolution)
- 각 픽셀을 주변 픽셀의 선형 결합(내적)으로 나타냄
- 선형 결합을 위한 오퍼레이터는 커널, 마스크 또는 필터라고 부른다.

3. CNN 개요
CNN은 Convolution Neural Network으로 합성곱 신경망이라고 한다.
CNN은 오랜 역사를 지니고 있으며 최근에 딥러닝의 붐을 불러오는데 중요한 역할을 했다.
CNN은 시각피질의 특징 추출을 위한 계층적인 처리 구조와 국소적인 특징 추출 등을 모사했다.
컴퓨팅 필요량의 최소화를 통해 주로 영상/비전 영역에서 큰 강점을 지님.
가. CNN의 기술적 배경
이미지를 보고서 시각적으로 무언가를 인식할 때, 특징들은 전체 이미지에서 아주 작은 영역에 위치한다.
또한 동일한 특징은 이미지마다 다른 곳에서 나타날 수 있다.
이에 CNN은 컨볼루션 기법을 도입했다.
- 특징 추출 단위를 전체 이미지가 아닌 그보다 작은 단위의 영역에 제한했다.
- 전체 이미지를 이 단위 영역으로 분리해 각각에 대해 특징 추출
나. CNN의 기술적 특징
전통적인 일반 신경망과 비교해서 CNN은 특징 추출에 다른 점이 있다.
부분 연결 방식을 사용해서 특징 추출에 작은 단위 영역만 고려함으로써 작은 수의 파라미터만 고려하면 된다.

또 필터 자체를 학습의 대상으로 본다.
이에 자동으로 다양한 특징을 추출해서 이를 필터를 조정한다.
다. CNN의 기본구조
CNN은 주로 Convolution, Pooling(Subsampling), Fully-connected 계층으로 구성된다.

4. 합성곱 계층
가. CNN의 합성곱 연산
입력 데이터에 필터를 이동하면서 반복적으로 적용해서 특징맵을 출력한다.
이동 방향은 좌에서 우, 상에서 하로 이동한다.
필터는 입력 데이터의 경계를 넘어서지 않는다. (Only fully-overlapped)
1) 스트라이드 (Stride)
: 합성곱은 차원별로 필터를 동일한 간격으로 이동시키면서 각각 실행하는데 이 간격을 스트라이드라 한다.
아래는 스트라이드 2의 경우.
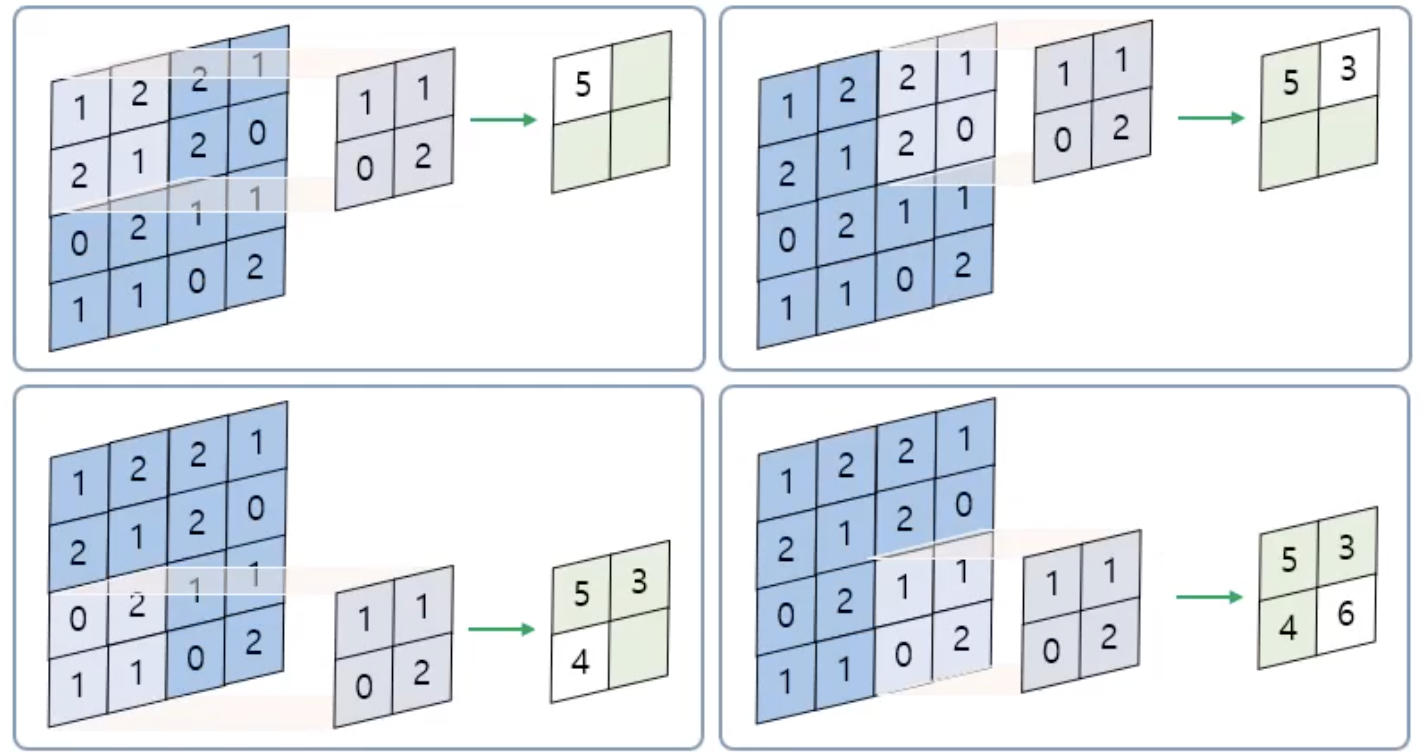
2) 패딩 (Padding)
: 입력 이미지 둘레에 일정한 크기의 데이터를 덧붙이는 것. 합성곱으로 인해 출력의 크기가 줄어드는 것을 방지하기 위함.

결과적으로 패딩은 출력의 크기를 증가시키고, 스트라이드는 감소시키는 효과가 있다.
나. 합성곱 계층
- 입력은 다차원 가능 (다수의 채널)
- 필터는 여러 개 사용할 수 있으며, 각각 독립적으로 1개의 특징맵을 생성하고
- 필터는 입력과 항상 동일 형상(형상은 같지만 크기는 다를 수 있음)
다. 합성곱 계층의 신경망 표현
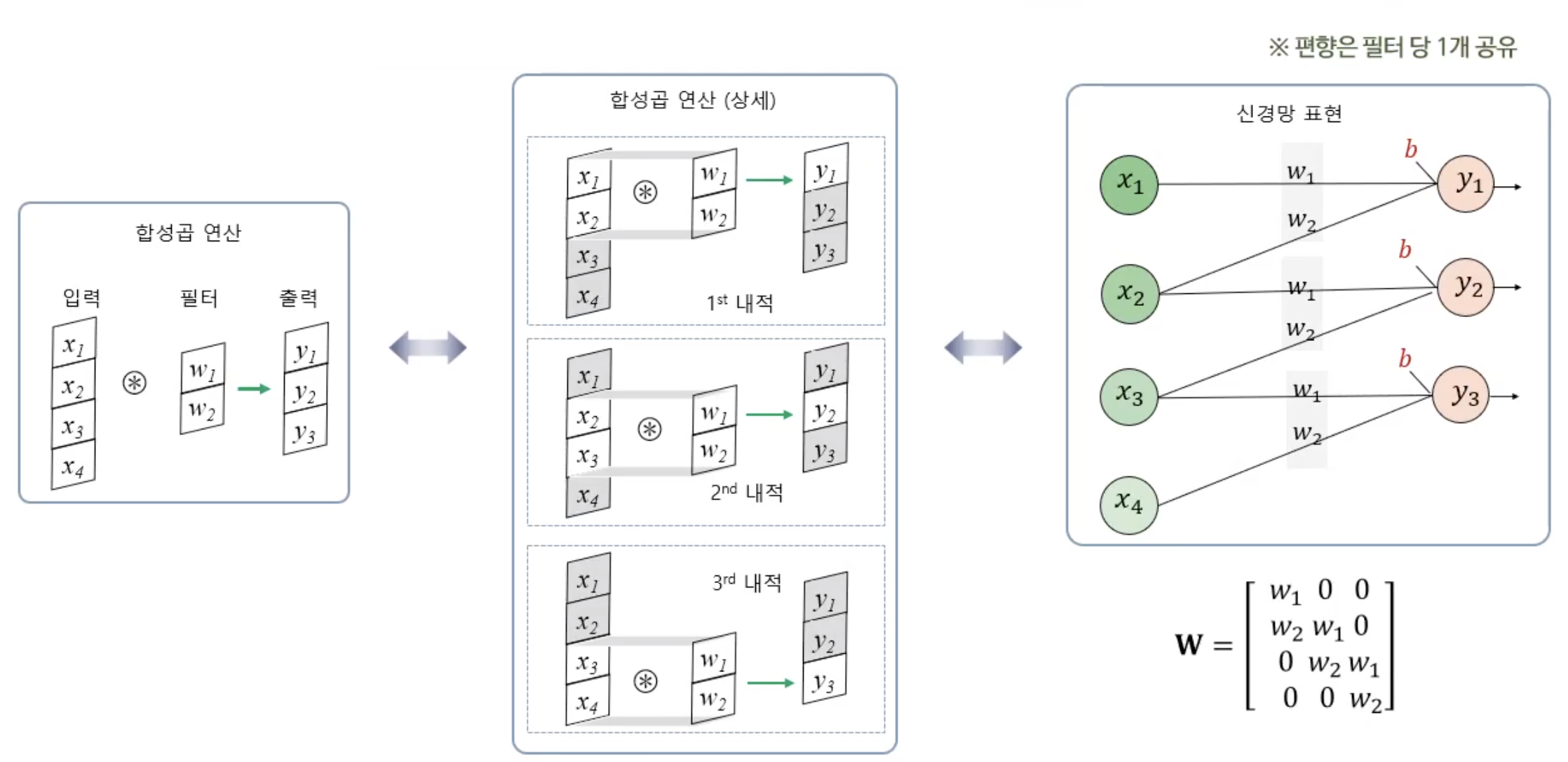
필터가 가중치이자 학습의 대상이다.
특징을 뽑아내는 필터를 생성하는 것이 CNN 훈련의 목적이다.
라. 합성곱 계층의 종류
- 일반 합성곱 계층 : 99.9%로 여기에 해당
- 국소 합성곱 계층(Locally connected) : 필터의 종류 개수에 따른 변형
- 경사 합성곱 계층 (Tilted connected) : 일반 합성곱과 국소 합성곱 계층의 조합
5. 풀링(서브 샘플링) 계층
가. 도입 배경
풀링 계층을 사용하는 가장 큰 이유는 풀링 계층은 특징맵의 공산 해상도를 축소시켜 연산량을 감소시킬 수 있기 때문이다.
풀링은 서브 샘플링(Subsampling)이라고도 불린다.
부수적인 효과로 일부 특징의 이동, 잡음, 왜곡 현상(Shift, Noise, Distortion)에 대한 강인성(Invariance)을 향상시키는 부수적 효과도 있음.
나. 풀링(서브 샘플링) 연산
합성곱과 비슷하지만 다른 점이 있다.
풀링 계층은 출력 특징맵의 크기를 줄이는 것이 목적이다.
이에 일반적으로 스트라이드와 풀링영역(풀링윈도우)의 크기가 동일하다.
또한 학습 파라미터가 없다.
그리고 입력 특징맵과 출력 특징맵의 차원은 같다는 특징이 있다.

다양한 종류의 풀링 연산이 있다.
예를 들어 풀링 영역 내에서 가장 최댓값을 고르는 연산부터 산술 평균, 기하 평균을 구하는 연산 등등이 있다.
다. 풀링 계층의 신경망 표현
가중치 없는 가상 연결선 및 풀링 연산을 수행하는 노드로 구성된다.
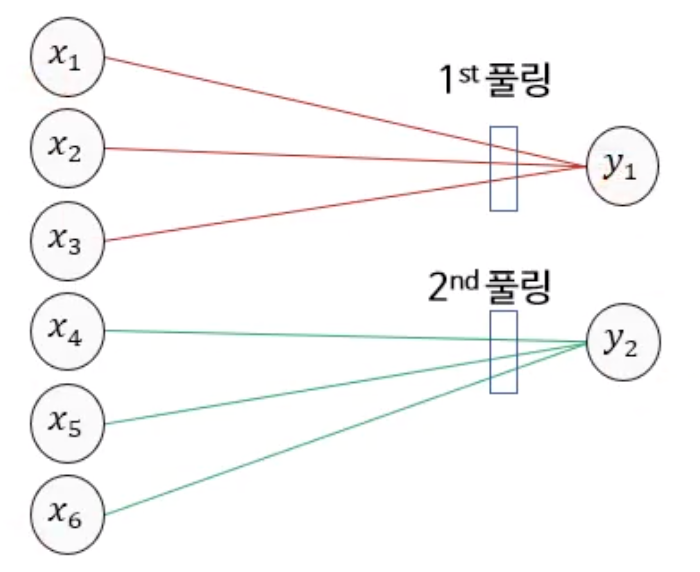
이미지 출처 : 대구대 AI입문 강의 9주차 강의
'학부 강의 > AI 입문' 카테고리의 다른 글
| 2023-01-02 AI입문_10 (0) | 2023.01.02 |
|---|---|
| 2022-11-13 AI입문_9 (0) | 2022.11.13 |
| 2022-11-05 AI입문_7 (0) | 2022.11.06 |
| 2022-10-13 AI입문_6 (0) | 2022.10.13 |
| 2022-10-05 AI입문_5 (0) | 2022.10.05 |